The Medium-Run Natural Interest Rate and the Short-Run Natural Interest Rate

Note: This post was the lead-up to my post “On the Great Recession.” After reading this one, I strongly recommend you take a look at that post.

Online, both in the blogs and on Twitter, I see a lot of confusion about the natural interest rate. I think the main source of confusion is that there is both a medium-run natural interest rate and a short-run natural interest rate. Let me define them:

  • medium-run natural interest rate: the interest rate that would prevail at the existing levels of technology and capital if all stickiness of prices and wages were suddenly swept away. That is, the natural rate of interest rate is the interest rate that would prevail in the real-business cycle model that lies behind a sticky-price, sticky-wage, or sticky-price-and-sticky-wage model.
  • short-run natural interest rate: the rental rate of capital, net of depreciation, in the economy’s actual situation. From here on, I will shorten the phrase “real rental rate of capital, net of depreciation” to  "net rental rate.“ 

Both the short-run and medium-run natural interest rates are distinct from actual interest rate, but in the short run, the short-run natural interest rate is much more closely linked to the actual interest rate than the medium-run natural interest rate is.

The Long Run, Medium Run, Short Run and Ultra Short Run

Introductory macroeconomics classes make heavy use of the concepts of the "short run” and the “long run.” To think clearly about economic fluctuations at a somewhat more advanced level, I find I need to use these four different time scales:

  • The Ultra Short Run: the period of about 9 months during which investment plans adjust–primarily as existing investment projects finish and new projects are started–to gradually bring the economy to short-run equilibrium. 
  • The Short Run: the period of about 3 years during which prices (and wages) adjust gradually bring the economy to medium-run equilibrium.
  • The Medium Run: the period of about 12 years during which the capital stock adjusts gradually to bring the economy to long-run equilibrium. 
  • The Long Run: what the economy looks like after investment, prices and wages, and capital have all adjusted. In the long run, the economy is still evolving as technology changes and the population grows or shrinks.  

Obviously, this hierarchy of different time scales reflects my own views in many ways. And it is missing some crucial pieces of the puzzle. Most notably, I have left out entry and exit of firms from the adjustment processes I listed. I don’t know have fast that process takes place. It could be an important short-run adjustment process, or it could be primarily a medium-run adjustment process. Or it could be somewhere in between.

The Medium-Run Natural Interest Rate

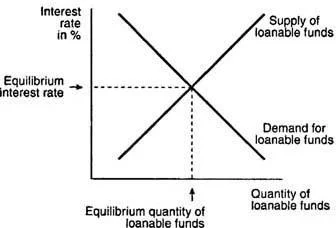
The importance of the medium-run natural interest rate is this: it is the place the economy will tend to once prices and wages have had a chance to adjust–as long as those prices and wages adjust fast enough that the capital stock won’t have changed much by the time that adjustment is basically complete. (I called that last assumption the “fast-price adjustment approximation” in my paper “The Quantitative Analytics of the Basic Neomonetarist Model”–the one paper where I had a chance to use the name of my brand of macroeconomics: Neomonetarism. See my post “The Neomonetarist Perspective” for more on Neomonetarism. The fast-price adjustment approximation is what makes good math out of the distinction between the short run and the medium run.)  The medium-run natural interest rate is not a constant. Indeed, at the introductory macroeconomics level, the standard model of the market for loanable funds is a model of how the medium-run natural interest rate is determined. Here is the key graph for the market for loanable funds, from the Cliffsnotes article on “Capital, Loanable Funds, Interest Rate”:

A common mistake students make is to try to use the market for loanable funds graph to try to figure out what the interest rate will be in the short run. That doesn’t work well. Although technically possible, it would be confusing, since how far the economy is above or below the natural level of output has a big effect on both the supply and the demand for loanable funds that using the market for loan. To understand the short-run natural interest rate, it is much better to use a graph designed for that purpose–a graph that focuses on how the short-run natural interest rate is determined by the demand for capital to use in production and by monetary policy.

The Short-Run Natural Interest Rate

Above, I defined the short-run natural interest rate as the "rental rate of capital, net of depreciation,“ or "net rental rate,” for short. What does this mean?

Renting Capital. First, to understand what it means to rent capital, think of those ubiquitous office parks. If the capital a company or other firm needs is an office to work in, it can rent one in an office park like this:

In retail, the capital a firm needs to rent might be retail space in a strip mall:

If a firm is in construction or landscaping, the capital it needs might be a bulldozer, which it can rent from the Cat Rental Store, among other places.

Of course, sometimes a firm needs specialized machine that it has to buy, because those machines are hard to rent. In that case, let me treat it as two different firms: one that buys the specialized machine and puts it out for rent, and another firm that rents the machine. The same trick works for a specialized building that is hard to rent, such as a factory designed for a particular type of manufacturing. When firms that own buildings or machinery are short of cash, sometimes they separate themselves into exactly these two pieces, and sell the piece that owns the specialized buildings or machines so the other piece of the firm can get the cash from the sale of those buildings or machines, while still being able to use those buildings and machines by paying to rent them.  

The (Gross) Rental Rate. I will call the gross rental rate simply “the rental rate." The rental rate is equal to the rent paid on a building or piece of equipment divided by the purchase price of that building or piece of equipment.  Because this is one price (expressed for example in dollars per year) divided by another price (dollars per machine), the rental rate is a real rate–that is, it does not need to be adjusted for inflation. The rental rate is usually expressed in percent per year, meaning the percent of the purchase price that has to be paid every year in order to rent the machine.  

The Net Rental Rate. It is useful to adjust the rental rate for depreciation, however. The paradigmatic case of depreciation is physical depreciation: a machine or building wearing out. More generally, a machine or building might become obsolete or start to look worse in comparison with newer machines. I am going to treat obsolescence as a form of depreciation. Obsolescence shows up in the price of new machines or buildings of that type falling relative to the prices of other goods in the economy. There are other things that can affect the prices of machines and buildings that will matter for the story below, but the rate of physical depreciation and the rate of obsolescence measured by declines in the real price of new machines and buildings of given types at the long-run trend rate are the two to subtract from the rental rate to get the net rental rate.

The Determination of Physical Investment

Physical investment is the creation of new capital–such as machines, buildings, software, etc.–that can be used as factors of production to help produce goods and services. Notice that I am using the phrase "physical investment” to distinguish what I am talking about from “financial investment.” So in this case, at some violence to the English language, I include writing new software in “physical investment." 

The amount of physical investment is determined by the costs and benefits of creating new machines, buildings, software, etc. now instead of later. Say we are talking about whether to create or purchase a building or machine now, or a year from now. The benefit of creating a new building or machine a year earlier is the rent that building or machine could earn in that year. In the absence of capital and investment adjustment costs (to which I return below), the cost of creating a new building or machine a year earlier is 

  • interest on the amount paid to create or purchase the building or machine.
  • physical depreciation
  • obsolescence

Dividing all of the costs and benefits by the amount paid to create or purchase the building or machine, the costs and benefits per dollar spent on the machine are 

benefit relative to amount spent = rental rate

cost relative to amount spent = real interest rate + physical depreciation rate + obsolescence rate

The reason it is the real interest rate in the cost relative to amount spent is because the obsolescence rate is being measured in terms of a real price decline.

In the absence of capital and investment adjustment costs, the rule for physical investment is:

  • If the rental rate is less than (the real interest rate + physical depreciation rate + obsolescence rate), invest later.
  • If the rental rate is more than (the real interest rate + physical depreciation rate + obsolescence rate), invest now.

If I move the physical depreciation rate and the obsolescence rate to the other side of the comparison, I can say the same thing this way: 

  • If the rental rate net of net of physical depreciation and obsolescence is below the real interest rate, invest later.
  • If the rental rate net of physical depreciation and obsolescence is above the real interest rate, invest now.

Or more concisely: 

  • If the net rental rate is less than the real interest rate, invest later.
  • If the net rental rate is more than the real interest rate, invest now.

Finally, using the definition of the short-run natural interest rate as the net rental rate and flipping the order, I can describe the rule for investment this way:

  • If the real interest rate is above the short-run natural interest rate (the net rental rate), invest later.
  • If the real interest rate is below the short-run natural interest rate (the net rental rate), invest now.

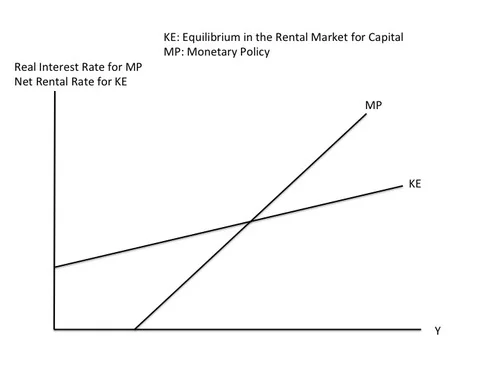
The Determination of the Short-Run Natural Interest Rate: Capital Equilibrium (KE) and Monetary Policy (MP)

Susanto Basu and I have a rough working paper on the determination of the short-run natural interest rate and about very-short-run movements of the actual interest rate in relation to the short-run natural interest rate: 

"Investment Planning Costs and the Effects of Fiscal and Monetary Policy” by Susanto Basu and Miles Kimball.

 We also have a set of slides to go along with the paper:

Slides for “Investment Planning Costs and the Effects of Fiscal and Monetary Policy” by Susanto Basu and Miles Kimball.

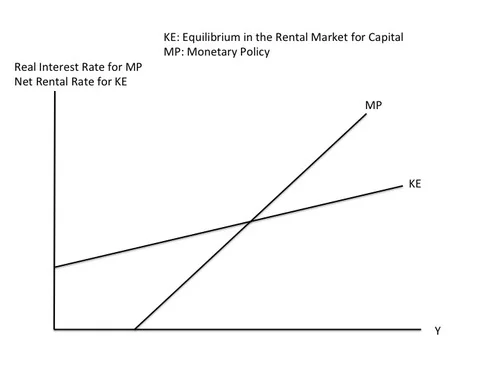
The short-run natural interest rate is determined by (a) equilibrium in the rental market for capital and (b) monetary policy.

Capital Equilibrium (KE): Supply and Demand for Capital to Rent

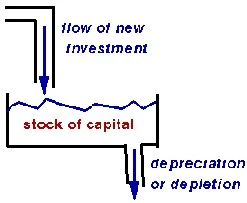
The Supply of Capital to Rent: The supply of capital to rent cannot change very fast. It takes time to create enough new machines, buildings, software, etc. through physical investment to affect the total amount of capital available to rent in any significant way. Wikipedia has an excellent article “Stock and flow” about this relationship between capital and physical investment. The canonical illustration is this picture of a bathtub:

Turning the tap on full blast might double the flow of water, but it will still take time for that flow to significantly affect the overall level of water in the tub. Similarly, turning investment on full blast may double the rate of physical investment creating new machines, buildings, software, etc., but it will still take time to significantly affect the overall amount of capital that exists in the form of machines, buildings, software, etc.

The Demand for Capital to Rent: The most important thing to understand about the demand for capital to rent is that it is higher in booms than in recessions. The more goods and services people want to buy, the more capital firms will want to rent at any given rental price in order to produce those goods and services. Ask any business person who has been involved in a decision to buy capital and they will tell you that they are more eager to get hold of capital to use when business is good than when business is bad.

The way I think of why the demand for capital to rent is higher in a boom than in a recession is this:

  • Since profit is revenue minus cost, whatever amount of output a profit-maximizing firm decides to produce to sell or inventory, it should try to produce that amount of output at the lowest possible cost. 
  • In a boom a firm will produce more output than in a recession (other things equal).
  • Since the stock of capital can’t change very fast, when the economy booms and firms add worker hours, a typical firm will not have as much capital per unit of labor as before. 
  • The more the economy booms, the higher wages  will be. (How much depends on whether wages are sticky or not. On sticky wages, if you are prepared for a hardcore economics post, see “Sticky Prices vs. Sticky Wages: A Debate Between Miles Kimball and Matthew Rognlie.”)
  • What is true of labor is also true for intermediate goods firms use as material inputs into production: when the economy booms and firms buy more materials to use, a typical firm will not have as much capital per unit of material inputs as before. 
  • Also, the more the economy booms, the higher the price of intermediate goods used as material inputs will be. (How much depends on whether the prices of the material inputs are sticky or not.) 
  • When the typical firm has less capital per unit of other inputs, it will be more eager to rent capital at any given rental price. 
  • If the firm is employing more labor and using more of other inputs despite wages and other input prices being high, it will be especially eager to rent additional capital at a given rental price, since capital then is relatively cheaper than other inputs.

The math behind this story is in the Basu-Kimball paper “Investment Planning Costs and the Effects of Fiscal and Monetary Policy.” There, although it is not needed to get these results, for simplicity we use the fact that for Cobb-Douglas production functions, the ratio of how much a cost-minimizing firm spends on labor and on capital is fixed. (See the relatively hardcore post “The Shape of Production: Charles Cobb’s and Paul Douglas’s Boon to Economics.”) Using the letters

  • R for the the rental rate,
  • K for the amount of capital,
  • W for the wage, and
  • L for the amount of total worker hours,

that means

RK = constant * WL.

Dividing both sides of this equation gives an equation for the rental rate:

R = constant * WL/K.

Since the total amount of capital K in the economy can’t change very fast, the total amount of capital in the typical firm also can’t change fast, so increases in wages W and total worker hours will push up the rental rate. And the net rental rate will parallel the overall gross rental rate very closely.  

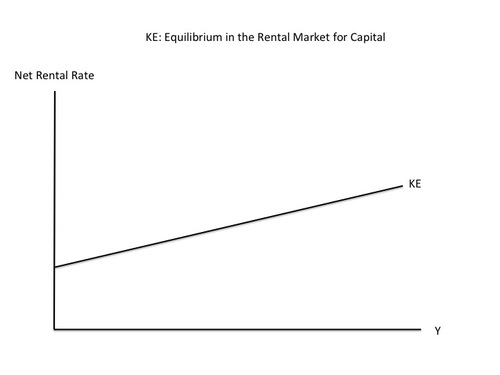
The KE Curve. With the supply of capital relatively fixed (or technically “quasi-fixed”) at any moment in time, a higher demand for capital means a higher equilibrium rental rate in the market for renting capital. How much a  typical firm chooses to produce is closely related to how much output the economy as a whole produces.  (Indeed, the amount firms produce must add up to the amount of output in the economy as a whole.) So the overall gross rental rate–and the net rental rate–will be increasing in the amount of output the economy as a whole produces. And of course, the amount of output the economy as a whole produces is GDP, for which we will use the single letter y.  Thus, the graph below, which has GDP on the horizontal axis, and like the graph at the top of this post, shows an upward slope for the KE curve:

The KE Curve vs. the IS Curve. The IS curve has no microfoundations. The KE curve does. That is, I just explained where the KE curve comes from. The explanations of where the IS curve comes from are either incoherent, or really imply something very different from the IS curve taught in introductory and intermediate macroeconomics classes. Let me critique several ways people convince themselves the IS curve is OK. (Don’t worry if you haven’t heard of some of the interpretations I am critiquing.)

  • The consumption Euler equation as an IS curve: The consumption Euler equation is an equation about changes rather than levels. Much more seriously, the consumption Euler equation acts like some sort of IS curve only in models that don’t have investment or other durables. Investment and other durables play such a big role in economic fluctuations that it It is hard to take a model of economic fluctuations that leaves out investment and other durables seriously. Bob Barsky, Chris House and I show how big a difference it makes to sticky price models to bring in investment or other durables goods in our paper “Sticky-Price Models and Durables Goods,” which appears in the American Economic Review.
  • Q-theory as a foundation for the IS curve: Like the consumption Euler equation, Q-theory yields a dynamic equation, instead of one that can be drawn as a simple curve with output on the horizontal axis and the real interest rate on the vertical axis. Q-theory says that firms might invest now even if the interest rate is above the net rental rate as long as the level of investment is increasing over time. The reason is that it will be harder to invest later when investment is proceeding faster, so it could make sense to get a jump on things and invest now. On the other hand, firms might delay investment even if the interest rate is below the net rental rate if the level of investment is decreasing over time. The reasons is that it will be easier to invest later when investment is proceeding more slowly, so it could make sense to wait until later when investment can be done in a more leisurely way. Suppose that we show the short-run equilibrium in terms of output and the real interest rate (rather than the net rental rate) and that higher investment is associated with higher GDP, as is usually the case. Then in relation to the KE curve, what Q-theory means is that the short-run equilibrium can be above the KE curve if that equilibrium point is moving to the right (GDP is increasing along with investment), while the short-run equilibrium can be below the KE curve if the equilibrium point is moving to the left (GDP is decreasing along with investment). But the slower the equilibrium point is moving, the closer it has to be to the KE curve. So when the “short-run” lasts a long time, as it has in the last five years since the bankruptcy of Lehman Brothers, the short-run equilibrium needs to be quite close to the KE curve. I discuss how the speed with which the economy is headed toward the medium-run equilibrium affects what can be gotten out of the Q-theory story in “The Quantitative Analytics of the Basic Neomonetarist Model.”
  • Heterogeneity of investment projects as a foundation for the IS curve: Heterogeneous investment projects, with some being able to clear a high interest-rate hurdle and some only being able to clear a low-interest-rate hurdle is the traditional story for the IS curve. This is actually a very interesting story, and one my coauthors Bob Barsky, Rudi Bachmann and I have been thinking about for a project in the works, but it actually points to something much more complex than an IS curve. For example, if potential investment projects are heterogeneous, then in general, one needs to keep track of how many are still available of each type. In any case, there is nothing simple about such a story.

The MP Curve. Central banks periodically meet to determine the interest rate they will set. The rate they set is a nominal interest rate, where “nominal” just means it is the interest rate that non-economists think of. The real interest rate is the nominal interest rate minus expected inflation. Inflation expectations tend to change quite slowly and sluggishly, so the nominal interest rate the central bank chooses determines the real interest rate in the short run and the very short run. Central banks ordinarily raise their interest rate target when the economy is booming and lower it when the economy is in recession, so the interest rate (both nominal and real) will be upward sloping in output. Indeed, in order to make the economy stable, the central bank should make sure that the real interest rate goes up faster with output than the net rental rate does, so that, going from left to right, the MP curve showing how the central banks target interest rate depends on output cuts the KE curve from below, as shown in the complete KE-MP diagram:

In the KE-MP model, the intersection of the KE and MP curves is the short-run equilibrium of the economy. In short-run equilibrium, the real interest rate equals the net rental rate, or equivalently, the real interest rate equals the short-run natural interest rate.

The Ultra Short Run

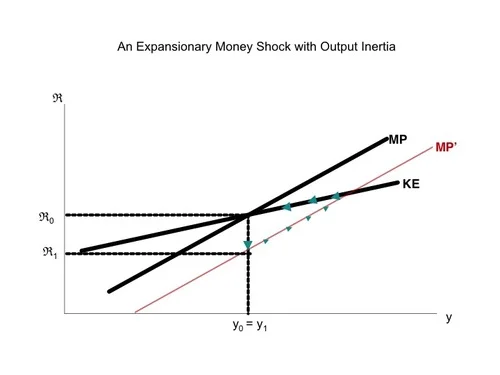
What brings the economy to short-run equilibrium is the adjustment of investment based on the gap between the net rental rate determined by the KE (capital rental market equilibrium) curve and the real interest rate determined by the MP (monetary policy) curve. But it takes time for firms to adjust their investment plans. Indeed, the level of investment is unlikely to adjust much faster than existing investment projects are completed and a new round of investment projects is started, as Susanto Basu and I discuss in “Investment Planning Costs and the Effects of Fiscal and Monetary Policy.” In the meanwhile, before investment has had time to full adjust, output can be away from its short-run equilibrium level, and the interest rate determined by the MP curve can be different from the net rental rate determined by the KE curve.   

For example, suppose that the economy starts out in short-run equilibrium, but then the central bank decides to make a change in the interest rate change for some reason other than a change in the level of output. Since output is unchanged, the change in the interest rate corresponds in the KE-MP model to a shift in the MP curve. The graph below, taken from Slides for “Investment Planning Costs and the Effects of Fiscal and Monetary Policy,” shows the effects of a monetary expansion.

The movement up along the MP’ curve reflects the ultra-short-run adjustment of investment to get to the new short-run equilibrium–a process that might take about 9 months. The movement back along the unchanging KE curve reflects the short-run adjustment of prices to get back to the original (and almost unchanged) medium-run equilibrium. Since the real interest rate is on the axis, the point representing first ultra-short-run equilibrium, and then short-run equilibrium, is always on the MP curve. (The graph does not show the gradual shift of the MP curve back to return the economy to the medium-run equilibrium. One way for that adjustment of the MP curve to happen is if there is some nominal anchor in the monetary policy rule so that the level of prices matters for monetary policy, not just the rate of change of prices.)

Why It Matters: Remarks About the KE-MP Model

  1. The reason I wrote this post is because many people don’t seem to understand that low levels of output lower the net rental rate and therefore lower the short-run natural interest rate. Leaving aside other shocks to the economy, monetary policy will not tend to increase output above its current level unless the interest rate is set below the short-run natural interest rate. That means that the deeper the recession an economy is in, the lower a central bank needs to push interest rates in order to stimulate the economy. In the Q-theory modification of the KE-MP model, the belief that the economy is going to recover fast could generate extra investment even if interest rates are somewhat higher, but when such confidence is lacking, the remedy is to push interest rates below the net rental rate that is the short-run natural interest rate.
  2. As discussed in “Investment Planning Costs and the Effects of Fiscal and Monetary Policy” and the Slides for “Investment Planning Costs and the Effects of Fiscal and Monetary Policy,” fiscal policy and technology shocks have counterintuitive effects on the KE curve. This is grist for another post. Also grist for another post is the way a version of the Keynesian Cross comes into its own in the ultra short run, but only during the 9 months or so of the ultra short run.  
  3. If a country makes the mistake of having a paper currency policy that prevents it from lowering the nominal interest rate below zero, then the MP curve has to flatten out somewhere to the left. (The zero lower bound on the nominal interest rate puts a bound of minus expected inflation on the real interest rate. That makes the floor on the real interest rate higher the lower inflation is.) The lower bound on the MP curve might then make it hard to get the interest rate below the net rental rate (a.k.a. the short-run natural interest rate). In my view, this is what causes depressions. QE can help, but is much less powerful than simply changing the paper currency policy so that the nominal interest rate can be lowered below the short-run natural interest rate, however low the recession has pushed that short-run natural interest rate.  (See the links in my post “Electronic Money, the Powerpoint File” and all of my posts on my electronic money sub-blog.)

Cathy O'Neil on Slow-Cooked Math

Math is sometimes better when it is marinated and cooked slowly; timeless truths take time. Cathy O'Neil, who blogs as Mathbabe, makes that point in her Q&A post  “How do I know if I’m good enough to go into math?” She kindly gave me permission to reblog it here. I talk about my own experiences after the text of her post. 

Q:

Hi Cathy,

I met you this past summer, you may not remember me. I have a question.

I know a lot of people who know much more math than I do and who figure out solutions to problems more quickly than me. Whenever I come up with a solution to a problem that I’m really proud of and that I worked really hard on, they talk about how they’ve seen that problem before and all the stuff they know about it. How do I know if I’m good enough to go into math?

Thanks, High School Kid

A: 

Dear High School Kid,

Great question, and I’m glad I can answer it, because I had almost the same experience when I was in high school and I didn’t have anyone to ask. And if you don’t mind, I’m going to answer it to anyone who reads my blog, just in case there are other young people wondering this, and especially girls, but of course not only girls.

Here’s the thing. There’s always someone faster than you. And it feels bad, especially when you feel slow, and especially when that person cares about being fast, because all of a sudden, in your confusion about all sort of things, speed seems important. But it’s not a race. Mathematics is patient and doesn’t mind. Think of it, your slowness, or lack of quickness, as a style thing but not as a shortcoming.

Why style? Over the years I’ve found that slow mathematicians have a different thing to offer than fast mathematicians, although there are exceptions (Bjorn Poonen comes to mind, who is fast but thinks things through like a slow mathematician. Love that guy). I totally didn’t define this but I think it’s true, and other mathematicians, weigh in please.

One thing that’s incredibly annoying about this concept of “fastness” when it comes to solving math problems is that, as a high school kid, you’re surrounded by math competitions, which all kind of suck. They make it seem like, to be “good” at math, you have to be fast. That’s really just not true once you grow up and start doing grownup math.

In reality, mostly of being good at math is really about how much you want to spend your time doing math. And I guess it’s true that if you’re slower you have to want to spend more time doing math, but if you love doing math then that’s totally fine. Plus, thinking about things overnight always helps me. So sleeping about math counts as time spent doing math. 

[As an aside, I have figured things out so often in my sleep that it’s become my preferred way of working on problems. I often wonder if there’s a “math part” of my brain which I don’t have normal access to but which furiously works on questions during the night. That is, if I’ve spent the requisite time during the day trying to figure it out. In any case, when it works, I wake up the next morning just simply knowing the proof and it actually seems obvious. It’s just like magic.]

So here’s my advice to you, high school kid. Ignore your surroundings, ignore the math competitions, and especially ignore the annoying kids who care about doing fast math. They will slowly recede as you go to college and as high school algebra gives way to college algebra and then Galois Theory. As the math gets awesomer, the speed gets slower.

And in terms of your identity, let yourself fancy yourself a mathematician, or an astronaut, or an engineer, or whatever, because you don’t have to know exactly what it’ll be yet. But promise me you’ll take some math major courses, some real ones like Galois Theory (take Galois Theory!) and for goodness sakes don’t close off any options because of some false definition of “good at math” or because some dude (or possibly dudette) needs to care about knowing everything quickly. Believe me, as you know more you will realize more and more how little you know.

One last thing. Math is not a competitive sport. It’s one of the only existing truly crowd-sourced projects of society, and that makes it highly collaborative and community-oriented, even if the awards and prizes and media narratives  about “precocious geniuses” would have you believing the opposite. And once again, it’s been around a long time and is patient to be added to by you when you have the love and time and will to do so.

Love,  Cathy

I especially like what Cathy says about fast and slow. I think of myself as a slow mathematician. It often takes me half an hour to wrap my head around a math problem or much more if it is a big one. I have gotten used to the confusion I regularly experience for that first chunk of time. If I keep wrestling with the problem, and come at it from different angles, usually the mental fog eventually clears.

Jing Liu: Show Kids that Solving Math Problems is Like Being a Detective

Jing Liu, Study Development Specialist at the Michigan Institute for Clinical and Health Research at the University of Michigan

Noah and I have received a flood of overwhelmingly positive email about our Quartz column ”There’s One Key Difference between Kids Who Excel at Math and Those Who Don’t.” I am very gradually making my way through the electronic pile. I was delighted to read near the top of the pile this note from Jing Liu, which has an insight into math education that seems right on the mark to me. Jing kindly gave permission to reprint a slightly revised version of her note here.

I just read the article that you and Noah Smith wrote on Quartz,

“There’s One Key Difference Between Kids Who Excel at Math and Those Who Don’t.”

 I’m writing to you because this is an issue that is close to my heart and I have been thinking about it for a long time.  I have two kids in K-12 schools, both love math, and I have been worried about what they are learning at school for years. I have talked with teachers and school principles and, of course, many parents.  A lot of the things that I’ve heard are concerning and reflect a general lack of  understanding from the educators on what math really is and what math can do for students who will not be mathematicians. I finally started a math enrichment program at our neighborhood elementary school and have taught advanced 4th and 5th graders through that program for four years now (this is my main community volunteer work).  So I’m sure you can tell why articles such as yours really strike a chord with me.

The issues that you raised in your article are all excellent and educators and parents should think hard about them. I’m also glad that you mentioned the starkly different attitudes toward sports and toward math.  It’s not that Americans don’t understand the value of hard work and that effort can definitely make up (to a certain extent) for lack of talent, it’s just that this somehow gets lost in math education. But I also think that there are another couple of very important issues that contribute no less to the current state of math education:

  1. There is a tendency to treat math as a set of discrete skills, procedures and facts for students to learn each year, not as a coherent and logical way of thinking that students will develop continuously through the years. The amount of rote memorization is, honestly, overwhelming. It is also quite clear that some teachers think that solving math problems is to follow a series of set steps. They miss the point that solving math problems is actually a quite creative process, in which one assesses the situation, assesses the tools in his/her toolboxes and zeros in gradually on how to connect what one knows and what one needs to know. It’s a detective’s work. So the question is: even if we make the kids not fear math, even if they are willing to work hard on math, are they truly learning the essence of math in the classrooms?                                                                                                             
  2. The strong tendency to protect kids from feeling deficient also affects those who are perceived to be capable math students. The math work tends to be very simple, kids are kept at a low level for a very long time until they are absolutely sure that they “have got it”. The slow pace and the lack of depth and challenge at each level can really turn kids off, even for those who are very capable. I’ve read that a whopping 60% of American students actually think that they are not challenged enough in math. In today’s high-stakes college entrance game, it is probably detrimental for a student to score a 70 on a math test. But in many other countries, East Asian or not, 70 is a perfectly OK score for good students. They know that they will apply a large set of math concepts and skills in various ways for a long time, and each time they apply these concepts and skills they have an opportunity to be better at it, and they know that it’s OK to make mistakes. After all, who is a good math student? Someone who only solves very simple problems and gets them all correct? Or someone who tackles very challenging problems but sometimes gets it wrong? In the US, the lack of challenge in the content, the lack of appreciation of math as a creative yet logical endeavor, and the high-stakes evaluation system together might just breed students who are risk-averse in their academic pursuit and who don’t get to see the true beauty of math. And this might be one reason why even the advanced students can be ill-prepared in math.

Quartz #36—>There's One Key Difference Between Kids Who Excel at Math and Those Who Don't

Here is the full text of my 36th Quartz column, and 2d column coauthored with Noah Smith, “There’s One Key Difference Between Kids Who Excel at Math and Those Who Don’t.” I am glad to now bring it home to supplysideliberal.com, and Noah will post it on his blog Noahpinion as well. It was first published on October 27, 2013. Links to all my other columns can be found here. In particular, don’t miss my follow-up column

How to Turn Every Child into a “Math Person.”

The warm reception for this column has been overwhelming. I think there is a hunger for this message out there. We want to get the message out, so if you want to mirror the content of this post on another site, just include both a link to the original Quartz column and to supplysideliberal.com.

“I’m just not a math person.”

We hear it all the time. And we’ve had enough. Because we believe that the idea of “math people” is the most self-destructive idea in America today. The truth is, you probably are a math person, and by thinking otherwise, you are possibly hamstringing your own career. Worse, you may be helping to perpetuate a pernicious myth that is harming underprivileged children—the myth of inborn genetic math ability.

Is math ability genetic? Sure, to some degree. Terence Tao, UCLA’s famous virtuoso mathematician, publishes dozens of papers in top journals every year, and is sought out by researchers around the world to help with the hardest parts of their theories. Essentially none of us could ever be as good at math as Terence Tao, no matter how hard we tried or how well we were taught. But here’s the thing: We don’t have to! For high school math, inborn talent is just much less important than hard work, preparation, and self-confidence.

How do we know this? First of all, both of us have taught math for many years—as professors, teaching assistants, and private tutors. Again and again, we have seen the following pattern repeat itself:

  1. Different kids with different levels of preparation come into a math class. Some of these kids have parents who have drilled them on math from a young age, while others never had that kind of parental input.

  2. On the first few tests, the well-prepared kids get perfect scores, while the unprepared kids get only what they could figure out by winging it—maybe 80 or 85%, a solid B.

  3. The unprepared kids, not realizing that the top scorers were well-prepared, assume that genetic ability was what determined the performance differences. Deciding that they “just aren’t math people,” they don’t try hard in future classes, and fall further behind.

  4. The well-prepared kids, not realizing that the B students were simply unprepared, assume that they are “math people,” and work hard in the future, cementing their advantage.

Thus, people’s belief that math ability can’t change becomes a self-fulfilling prophecy.

The idea that math ability is mostly genetic is one dark facet of a larger fallacy that intelligence is mostly genetic. Academic psychology journals are well stocked with papers studying the world view that lies behind the kind of self-fulfilling prophecy we just described. For example, Purdue University psychologist Patricia Linehan writes:

A body of research on conceptions of ability has shown two orientations toward ability. Students with an Incremental orientation believe ability (intelligence) to be malleable, a quality that increases with effort. Students with an Entity orientation believe ability to be nonmalleable, a fixed quality of self that does not increase with effort.

The “entity orientation” that says “You are smart or not, end of story,” leads to bad outcomes—a result that has been confirmed by many other studies. (The relevance for math is shown by researchers at Oklahoma City who recently found that belief in inborn math ability may be responsible for much of the gender gap in mathematics.)

Psychologists Lisa Blackwell, Kali Trzesniewski, and Carol Dweck presented these alternatives to determine people’s beliefs about intelligence:

  1. You have a certain amount of intelligence, and you really can’t do much to change it.

  2. You can always greatly change how intelligent you are.

They found that students who agreed that “You can always greatly change how intelligent you are” got higher grades. But as Richard Nisbett recounts in his book Intelligence and How to Get It,they did something even more remarkable:

Dweck and her colleagues then tried to convince a group of poor minority junior high school students that intelligence is highly malleable and can be developed by hard work…that learning changes the brain by forming new…connections and that students are in charge of this change process.

The results? Convincing students that they could make themselves smarter by hard work led them to work harder and get higher grades. The intervention had the biggest effect for students who started out believing intelligence was genetic. (A control group, who were taught how memory works, showed no such gains.)

But improving grades was not the most dramatic effect, “Dweck reported that some of her tough junior high school boys were reduced to tears by the news that their intelligence was substantially under their control.” It is no picnic going through life believing you were born dumb—and are doomed to stay that way.

For almost everyone, believing that you were born dumb—and are doomed to stay that way—is believing a lie. IQ itself can improve with hard work. Because the truth may be hard to believe, here is a set of links about some excellent books to convince you that most people can become smart in many ways, if they work hard enough:

So why do we focus on math? For one thing, math skills are increasingly important for getting good jobs these days—so believing you can’t learn math is especially self-destructive. But we also believe that math is the area where America’s “fallacy of inborn ability” is the most entrenched. Math is the great mental bogeyman of an unconfident America. If we can convince you that anyone can learn math, it should be a short step to convincing you that you can learn just about anything, if you work hard enough.

Is America more susceptible than other nations to the dangerous idea of genetic math ability? Here our evidence is only anecdotal, but we suspect that this is the case. While American fourth and eighth graders score quite well in international math comparisons—beating countries like Germany, the UK and Sweden—our high-schoolers  underperform those countries by a wide margin. This suggests that Americans’ native ability is just as good as anyone’s, but that we fail to capitalize on that ability through hard work. In response to the lackluster high school math performance, some influential voices in American education policy have suggested simply teaching less math—for example, Andrew Hacker has called for algebra to no longer be a requirement. The subtext, of course, is that large numbers of American kids are simply not born with the ability to solve for x.

We believe that this approach is disastrous and wrong. First of all, it leaves many Americans ill-prepared to compete in a global marketplace with hard-working foreigners. But even more importantly, it may contribute to inequality. A great deal of research has shown that technical skills in areas like software are increasingly making the difference between America’s upper middle class and its working class. While we don’t think education is a cure-all for inequality, we definitely believe that in an increasingly automated workplace, Americans who give up on math are selling themselves short.

Too many Americans go through life terrified of equations and mathematical symbols. We think what many of them are afraid of is “proving” themselves to be genetically inferior by failing to instantly comprehend the equations (when, of course, in reality, even a math professor would have to read closely). So they recoil from anything that looks like math, protesting: “I’m not a math person.” And so they exclude themselves from quite a few lucrative career opportunities. We believe that this has to stop. Our view is shared by economist and writer Allison Schrager, who has written two wonderful columns in Quartz (here and here), that echo many of our views.

One way to help Americans excel at math is to copy the approach of the Japanese, Chinese, and Koreans.  In Intelligence and How to Get It,  Nisbett describes how the educational systems of East Asian countries focus more on hard work than on inborn talent:

  1. “Children in Japan go to school about 240 days a year, whereas children in the United States go to school about 180 days a year.”

  2. “Japanese high school students of the 1980s studied 3 ½ hours a day, and that number is likely to be, if anything, higher today.”

  3. “[The inhabitants of Japan and Korea] do not need to read this book to find out that intelligence and intellectual accomplishment are highly malleable. Confucius set that matter straight twenty-five hundred years ago.”

  4. “When they do badly at something, [Japanese, Koreans, etc.] respond by working harder at it.”

  5. “Persistence in the face of failure is very much part of the Asian tradition of self-improvement. And [people in those countries] are accustomed to criticism in the service of self-improvement in situations where Westerners avoid it or resent it.”

We certainly don’t want America’s education system to copy everything Japan does (and we remain agnostic regarding the wisdom of Confucius). But it seems to us that an emphasis on hard work is a hallmark not just of modern East Asia, but of America’s past as well. In returning to an emphasis on effort, America would be returning to its roots, not just copying from successful foreigners.

Besides cribbing a few tricks from the Japanese, we also have at least one American-style idea for making kids smarter: treat people who work hard at learning as heroes and role models. We already venerate sports heroes who make up for lack of talent through persistence and grit; why should our educational culture be any different?

Math education, we believe, is just the most glaring area of a slow and worrying shift. We see our country moving away from a culture of hard work toward a culture of belief in genetic determinism. In the debate between “nature vs. nurture,” a critical third element—personal perseverance and effort—seems to have been sidelined. We want to bring it back, and we think that math is the best place to start.

Follow Miles on Twitter at @mileskimball. Follow Noah at @noahpinion.

The Shakeup at the Minneapolis Fed and the Battle for the Soul of Macroeconomics

Here is a link to my 38th column on Quartz, coauthored with Noah Smith, “The shakeup at the Minneapolis Fed is a battle for the soul of macroeconomics–again.” Our editor insisted on a declarative title that seriously overstates our degree of certainty on the nature of the specific events that went down at the Minneapolis Fed. I toned it down a little in my title above.

Visionary Grit

blog.supplysideliberal.com tumblr_inline_mwjnlogxqg1r57lmx.png

Click here to watch the TEDTalk that inspired this post–Angela Duckworth’s talk “The Key to Success: The Surprising Trait That is MUCH More Important Than IQ.”

TED Weekends, which is associated with Huffington Post, asked me to write an essay on my reaction to Angela Duckworth’s wonderful talk about grit as the secret to success. Here is a link to my essay on TED Weekends:

Below is the full text of my essay. It pushes further the themes in the Quartz column I wrote with Noah Smith: “Power of Myth: There’s one key difference between kids who excel at math and those who don’t.”

Grit, more than anything else, is what makes people succeed. Psychologist Angela Duckworth, who has devoted her career to studying grit, defines grit this way:

Grit is passion and perseverance for very long-term goals. Grit is having stamina. Grit is sticking with your future, day in, day out, not just for the week, not just for the month, but for years – and working really hard to make that future a reality. Grit is living life like a marathon, not a sprint.

But where does grit come from? First, it comes from understanding and believing that grit is what makes people succeed:

  • understanding that persistence and hard work are necessary for lasting success, and
  • believing that few obstacles can ultimately stop those who keep trying with all of their hearts, and all of their wits.

But that is not enough. Grit also comes from having a vision, a dream, a picture in the mind’s eye, of something you want so badly, you are willing to work as hard and as long as it takes to achieve that dream. Coaches know how powerful dreams – dreams of making the team, of scoring a goal, of winning the game, or of winning a championship – can be for kids. Dreams of knowing the secrets of complex numbers, graduating from college, rising in a career, making a marriage work, achieving transcendence, changing the world, need to be powerful like that to have a decent chance of success.

Grit is so powerful that once the secret is out, a key concern is to steer kids toward visions that are not mutually contradictory. Not everyone can win the championship. Someone has to come in second place. But almost everyone can learn the secrets of complex numbers, graduate from college, rise in a career, make a marriage work, achieve transcendence, and change the world for the better.

What can adults do to help kids understand and believe that grit is what makes people succeed, and to help them find a vision that is powerful enough to motivate long, hard work? Noah Smith and I tried to do our bit with our column “Power of Myth: There’s one key difference between kids who excel at math and those who don’t.” We were amazed at the reception we got. Our culture may be turning the corner, ready to reject the vicious myth that out of any random sampling of kids, many are genetically doomed to failure at math, failure at everything in school, failure in their careers, or even failure at life. The amazing reception of Angela Duckworth’s TEDTalk is another good sign. But articles and TEDTalks won’t do the trick, because not everyone watches TEDTalks, and – as things are now – many people read only what they absolutely have to. So getting the word out that grit, not genes, is the secret to success, will take the work of the millions who do read and who do watch TEDTalks, to tell, one by one, the hundreds of millions in this country and in other countries with similar cultures about the importance of grit.

What can adults do to help kids get a vision that is powerful enough to motivate long, hard work? Many are already doing heroic work in that arena. But other would-be physicians among us must first heal ourselves. How many of us have a defeatist attitude when we think of the problems our nation and the world face? How many of us lack a vision of what we want to achieve that will motivate us to long, hard work, stretching over many years?

Visions don’t have to be perfect. It is enough if they are powerful motivators, and good rather than bad. And it is good to share our visions with one another. Here are some of the things that dance before my mind’s eye and motivate me: 1, 2. I hope everyone who reads this will think about how to express her or his own vision – a vision that motivates hard work to better one’s own life and to better the world. That is the example we need to set for the kids.

Lately, since I started reading and thinking about the power of hard, deliberate effort, I have been catching myself; when I hear myself thinking “I am bad at X” I try to recast the thought as “I haven’t yet worked hard at getting good at X.” Some of the skills I haven’t yet worked at honing, I probably never will; there are only so many hours in the day. But with others, I have started trying a little harder, once I stopped giving myself the easy excuse of “I am bad at X.” There is no need to exaggerate the idea that almost everyone (and that with little doubt includes you) can get dramatically better at almost anything. But if we firmly believe that we can improve at those tasks to which we devote ourselves, surprising and wonderful things will happen.

Among the many wonderful visions we can pursue with the faith that working hard – with all of our hearts and all of our wits – will bear fruit, let’s devote ourselves to getting kids to understand that grit is the key to success. Let’s help them find visions that will motivate them to put in the incredibly hard effort necessary to do the amazing things that they are capable of, and help them tap the amazing potential they have as human beings.

Ideas are not set in stone. When exposed to thoughtful people, they morph and adapt into their most potent form. TEDWeekends will highlight some of today’s most intriguing ideas and allow them to develop in real time through your voice! Tweet #TEDWeekends to share your perspective or email tedweekends@huffingtonpost.com to learn about future weekend’s ideas to contribute as a writer.

Learning to Do Deep Knee Bends Balanced on One Foot

I am 53 now and sometime think forward to some dangers of getting older. I read a few years ago that Tai Chi exercises improve balance enough to significantly reduce falls that can sometimes break older bones. I don’t know where to find time for Tai Chi itself in my schedule, so I cut corners. I just do a daily set of deep knee bends balanced on one foot: 18 reps on the right leg, and 20 reps on the left leg, because that one is weaker and needs more strengthening. I had a pretty tough time getting so I could do that many repetitions without toppling over again and again and having to catch myself with my hands. But gradually, gradually, I could do a few more repetitions in a row before toppling over, until now I don’t have too much trouble doing 18 or 20 in a row.

I think of this as a good analogy for a lot of learning: making mistakes and carefully correcting them, over and over again, until very gradually the number of mistakes diminishes. If you aren’t willing to fall–many times–in order to learn, you will fail.

Marc F. Bellemare's Story: "I'm Bad at Math"

Link to “I’m Bad at Math: My Story” on Marc’s blog

I think it is very valuable to share one another’s stories about what the idea that math ability is primarily genetic did to our lives. My story is at this link. Marc Bellemere wrote his story on his blog, and kindly agreed to let me publish it here on supplysideliberal.com as well.

Last week, Miles Kimball and Noah Smith, two economists (one at Michigan, one at Long Island) had a column on the Atlantic’s website (ht: Joaquin Morales, via Facebook) in which they took to task those who claim that math ability is genetic.

Kimball and Smith argue that that’s largely a cop-out, and that there is no such thing as “I’m bad at math.” Rather, being good at math is the product of good, old-fashioned hard work:

Is math ability genetic? Sure, to some degree. Terence Tao, UCLA’s famous virtuoso mathematician, publishes dozens of papers in top journals every year, and is sought out by researchers around the world to help with the hardest parts of their theories. Essentially none of us could ever be as good at math as Terence Tao, no matter how hard we tried or how well we were taught. But here’s the thing: We don’t have to! For high-school math, inborn talent is much less important than hard work, preparation, and self-confidence.

How do we know this? First of all, both of us have taught math for many years—as professors, teaching assistants, and private tutors. Again and again, we have seen the following pattern repeat itself:

  1. Different kids with different levels of preparation come into a math class. Some of these kids have parents who have drilled them on math from a young age, while others never had that kind of parental input.
  2. On the first few tests, the well-prepared kids get perfect scores, while the unprepared kids get only what they could figure out by winging it—maybe 80 or 85%, a solid B.
  3. The unprepared kids, not realizing that the top scorers were well-prepared, assume that genetic ability was what determined the performance differences. Deciding that they “just aren’t math people,” they don’t try hard in future classes, and fall further behind.
  4. The well-prepared kids, not realizing that the B students were simply unprepared, assume that they are “math people,” and work hard in the future, cementing their advantage.

Kimball and Smith’s column resonated deeply with me, because I discovered quite late (but just in time) that hard work trumps natural ability any day of the week when it comes to high-school math–if not when it comes to PhD-level math for economists.

My Story

What follows is a story which, although I have mentioned it to a few colleagues in the past, I’ve never told publicly until I posted it on my blog on November 6.

Until my early 20s, I never knew that one could become good at math. In high school, I failed tenth-grade math. That year, I’d had mono, so that provided a convenient excuse that I could use when I would tell people that I had to take tenth-grade math again in the summer.

That summer, though, I worked really hard at math, and I did very well, scoring something like a 96% score. But I ascribed my success to the people I was competing with rather than to my own hard work. The class, after all, was entirely composed of other failures, and in the kingdom of the blind, the one-eyed man is king.

When I began studying economics in college, I enrolled in a math for economists course the first semester. I quickly dropped out of it, thinking it was too difficult (and to be sure, the textbook was somewhat hardcore for a first course in math for economists). The following semester, I enrolled in the same course, which was taught by a different instructor, one who seemed a bit more laid-back and who taught it at a level that was better suited for someone like me.

As it turns out, that instructor was a Marxian, so one of the things he taught was the use of Leontief matrices, or input-output models. Like the clueless college student that I was back then, I decided that that stuff was not important, and so skipped studying it for the final.

Much to my surprise, 60% of the final was on Leontief matrices, and so I failed the course and had to take it again the next semester. Even that second time around, I didn’t do that great, scraping by with a C+ (which, if I recall correctly, was the average score in core econ major courses at the Université de Montréal back then).

After finally passing Math for Economists I, I realized I had to take Math for Economists II, which was reputed to be very difficult. But for some reason, it was then that I remembered my tenth-grade math summer course, and how my hard work had seemed to yield impressive results back then. So I decided to really apply myself in that second Math for Economists course, and I got an A.

When I saw my transcript that semester, I finally saw the light: I had been terrible at math all my life because I hadn’t worked hard at it; in fact, I hadn’t worked at all up until that point, and here I was, getting an A in one of the hardest classes in the major.

I graduated with a 3.2 GPA, which wasn’t great considering that my alma mater has a 4.3 scale. But it was enough to get admitted into the M.Sc. program in Economics at the Université de Montréal, and so I applied and got in. But then, I remembered that my hard work had paid off handsomely during my senior year, and I decided to apply myself in every single class. Lo and behold, I did well. So well, in fact, that I finished my M.Sc. with a 4.1 GPA, which allowed me not only to get admitted for a Ph.D. in Applied Economics at Cornell, but to get a full financial ride, including a fellowship for my first year.

Perhaps more importantly, my cumulative experience with the hard work–excellent results nexus boosted my confidence, and it taught me that I could do well in a graduate program in applied economics. Indeed, Cornell was then known for the difficulty of its qualifier in microeconomic theory (which was administered back then by the economics department and was on all of Mas-Colell et al. and more). In any given year, half of all the students (i.e., applied economics, business, and economics students) taking it would fail.

To be sure, I had to work very, very hard during my first year, but I managed to pass my qualifying exam the first time around (thankfully, us applied economics students didn’t have to take the macro qualifier; we only needed to get a B- in one of the core macro courses). In fact, many of my classmates who seemed to rely on their “natural” ability to do math (including folks who had been math majors in college) ended up failing the micro qualifier.

That series of successes followed by hard work was eventually what gave me the confidence to do a little bit of micro theory: in the first essay in my dissertation, I developed a dynamic principal-agent model to account for the phenomenon I was studying empirically. And ultimately, I published an article in the American Journal of Agricultural Economics (AJAE) that relied entirely on microeconomic theory (and thus on quite a bit of math), an article for which my coauthor and I won that year’s best AJAE article award.

Ironically enough, in that article, we cited Miles Kimball’s 1990 Econometrica paper on prudence.

Quartz #34—>Janet Yellen is Hardly a Dove—She Knows the US Economy Needs Some Unemployment

Link to the Column on Quartz

Here is the full text of my 34th Quartz column “Janet Yellen is Hardly a Dove–She Knows the US Economy Needs Some Unemployment” now brought home to supplysideliberal.com. It was first published on October 11, 2013. Links to all my other columns can be found here.

If you want to mirror the content of this post on another site, that is possible for a limited time if you read the legal notice at this link and include both a link to the original Quartz column and the following copyright notice:

© October 11, 2013: Miles Kimball, as first published on Quartz. Used by permission according to a temporary nonexclusive license expiring June 30, 2015. All rights reserved.

Below, after the text of the column as it appeared in Quartz, I note some of the reactions and explain some of the math behind the column.   

President Obama was right to say his appointment of Janet Yellen to head the US Federal Reserve has been one of his most important economic decisions. As the graph below shows, from the mid-1980s through 2007, monetary policy kept US GDP growth fairly steady, without needing much help from Keynesian fiscal policy. Economists talk about this period when GDP growth was much steadier than before as “The Great Moderation.” Monetary policy has done less well in years since the financial crisis in 2008, because the Fed felt it could not lower its target interest rate below zero, and has not been fully comfortable with its backup tools of quantitative easing and “forward guidance” about what it will do to interest rates years down the road.

Yellen’s academic research on the theory of unemployment points to one of the key reasons it is important to keep the growth of the economy steady. Let me explain.

With her husband George Akerlof, who was among recipients of the Nobel Prize in Economics in 2001, Yellen edited “Efficiency Wage Models of the Labor Market,” which gives one of the leading theories of why some level of unemployment persists even in good times, and why unemployment gets much worse in bad times. Yellen summarized the major variants of Efficiency Wage Theory. They all share the idea that firms often want to pay their workers more than their workers can get elsewhere. It might seem that employers would always want to pay workers as little as possible, but badly paid workers don’t care much about keeping their jobs.

Low pay affords workers an attitude of “Take this job and shove it!.” If workers have no reason to obey you because they are just as well off without the job—and owe you nothing—it will be hard to run a business. And if you hire someone at very low pay who actually sticks around, it is reasonable to worry about what is wrong with the worker that makes it so that worker can’t do better than the miserable job you are offering them. The way out of this trap is for an employer to pay enough that the worker is significantly better off with the job than without the job.

It might sound like a good thing that firms have a reason to pay workers more, except that, according to the Efficiency Wage Theory, firms have to keep raising wages until workers are too expensive for all of them to get hired. The reasoning goes like this: There will always be some jobs that are at the bottom of the heap. Suppose some of those bottom-of-the-heap jobs are also dead-end jobs, with no potential for promotion or any other type of advancement. If bottom-of-the-heap, dead-end jobs were free for the taking, no one would ever worry about losing one of those jobs. The Johnny Paycheck moment—when the worker says “Take this job and shove it”—will not be long in coming. If they were free for the taking, bottom-of-the-heap, dead-end jobs would also be subject to high turnover and low levels of emotional attachment to the firm.

The only way a bottom-of-the-heap, dead-end job will ever be worth something to a worker is if there is a something worse than a bottom-of-the-heap, dead-end job. In Efficiency Wage Theory, that something worse is being unemployed. To make workers care about bottom-of-the-heap, dead-end jobs, employers have to keep raising their wages above what other firms are offering until workers are expensive enough that there is substantial unemployment—enough unemployment that being unemployed is worse than having one of those bottom-of-the-heap, dead-end jobs. For the worker, Efficiency Wage Theory is bittersweet.

Some of what counts as unemployment in the official statistics arises from people in between jobs who simply need a little time to identify and decide among all the different jobs potentially available to them. And some is from people who have an unrealistic idea of what kinds of jobs are potentially available to them. But let me call the part of unemployment due to this Efficiency-Wage-Theory logic motivational unemployment. In the case of motivational unemployment, there will be people who are unemployed who are essentially identical to people who do have jobs. It is just bad luck on the part of the unemployed to be allotted the social role of scaring those who do have jobs into doing the boss’s bidding.

In criminal justice, swift, sure punishment does not need to be as harsh as slow, uncertain punishment. Just so, in Efficiency Wage Theory, the better and faster bosses are at catching worker dereliction of duty, the less motivational unemployment is needed. Because it is easier to motivate workers when worker dereliction of duty is detected more quickly, firms will stop raising wages and cutting back on employment at lower levels of unemployment.

There are other conceivable ways to reduce the necessity of motivational unemployment in the long run.

  1. If all jobs had advancement possibilities—that is, no jobs were dead-end jobs—it might be possible to motivate workers by the hope of moving up the ladder. This works best if workers actually learn and get better at what they do over time by sticking with a job.
  2. If doing what needs to be done on the job could be made more pleasant, it would reduce the need for the carrot of above-market wages or the stick of unemployment.
  3. If workers could trust firms not to cheat them and were required to pay for their jobs, they would be afraid of having to pay for a job all over again if they were fired.
  4. There could be a threat other than unemployment, such as deportation.
  5. Unemployment could be made less attractive.
  6. Worker’s reputations could be tracked more systematically and made available online.

To make possibilities 5 and 6 more concrete, let me mention online activist Morgan Warstler’s thought-provoking (if Dickensian and possibly unworkable) proposal that would make unemployment less attractive and would better track workers reputations: An “eBay job auction and minimum income program for the unemployed.” The program would require those receiving unemployment insurance or other assistance to work in a temp-job—within a certain radius from the worker’s home. The employer would go online to bid on an employee to hire and the wages would offset some of the cost of government assistance. Both the history of bids and an eBay-like rating system of the workers would give later employers a lot of useful information about the worker. Workers would also give feedback on firms, to help ferret out abuses. It is obvious that many of the policies that Efficiency Wage Theory suggests might reduce unemployment would be politically toxic and some (such as using the threat of deportation to keep employees in line) are morally reprehensible. But some of those policies merit serious thought.

What does Efficiency Wage Theory have to say about monetary policy? The details of how motivational unemployment works matter. Think about bottom-of-the-heap, dead-end jobs again. As the unemployment rate goes down in good times, the wage firms need to pay to motivate those workers goes up faster and faster, creating inflationary pressures. But the wages of those jobs at the bottom are already so low that when unemployment goes up in the bad times, it takes a lot of extra unemployment to noticeably reduce the wages that firms feel they need to pay and bring inflation back down. This is one of several, and possibly the biggest reason that the round trip of letting inflation creep up and then having to bring it back down is a bad deal. And a round trip in the other direction—letting inflation fall as it has in the last few years with the idea of bringing it back up later—is just as costly. (You can see the fall in what the Fed calls “core” inflation—the closest thing to being the measure of inflation the Fed targets—in the graph below.) It is much better to keep inflation steady by keeping output and unemployment at their natural levels.

The conventional classification divides monetary policy makers into “hawks,” who hate inflation more than unemployment and “doves” who hate unemploymentmore than inflation. Most commentators classify Janet Yellen as a dove. But I parse things differently. There can be serious debates about the long-run inflation target. I have taken the minority position that our monetary system should be adapted so that we can safely have a long-run inflation target of zero. But as long as there is a consensus on the Fed’s monetary policy committee that 2% per year (in terms of the particular measure of inflation in the graph above) is the right long-run inflation target, it is entirely appropriate for Janet Yellen to think that inflation below 2% is too low in any case, so that further monetary stimulus is beneficial not only because it lowers unemployment, but also because it raises inflation towards its 2% target level.

To see the logic, imagine some future day in which everyone agreed that the long-run inflation target should be zero. Then if inflation were below the target—in that case actually being deflation–then almost everyone would agree that monetary stimulus would be good not only because it lowered unemployment, but also because it raised inflation from negative values toward zero. Anyone who wants to make the case for a long-run inflation target lower than 2% should make that argument, but otherwise they should not be too quick to call Janet Yellen a dove for insisting that the Fed should keep inflation from falling below the Fed’s agreed-upon long-run inflation target of 2%.

Nor should anyone be called a hawk and have the honor of being thought to truly hate inflation if they are not willing to do what it takes to safely bring inflation down to zero and keep it there. Letting inflation fall willy-nilly because a serious recession has not been snuffed out as soon as it should have been is no substitute for keeping the economy on an even keel and very gradually bringing inflation down to zero, with all due preparation.

There is also no special honor in having a tendency to think that a dangerous inflationary surge is around the corner when events prove otherwise. One feather in Yellen’s cap is the Wall Street Journal’s determination that her predictions for the economy have been more accurate than any of the other 14 Fed policy makers analyzed. For the Fed, making good predictions about where the economy would go without any policy intervention, and what the effects of various policies would be, is more than half the battle. Differences in views about the relative importance of inflation and unemployment pale in comparison to differences in views about how the economy works in influencing policy recommendations. Having a good forecasting record is not enough to show that one understands how the economy works, but over time, having a bad forecasting record certainly indicates some lack of understanding—unless one is learning from one’s mistakes.

In the last 10 years, America’s economic policy-making apparatus as a whole made at least two big mistakes: not requiring banks to put up more of their own shareholders’ money when they took risks, and not putting in place the necessary measures to allow the Fed to fight the Great Recession as it should have, with negative interest rates. It is time for America’s economic policy-making apparatus to learn from its mistakes, on both counts.

As the saying goes, “It’s difficult to make predictions, especially about the future.” But I will hazard the prediction that if the Senate confirms her appointment, monetary historians 40 years from now will say that Janet Yellen was an excellent Fed chief. There will be more tough calls ahead than we can imagine clearly. As president of the San Francisco Fed from 2004 to 2010, and as vice chair of the Fed since then, Yellen has brought to bear on her role as a policymaker both skills in deep abstract thinking from her academic background and the deep practical wisdom also known as “common sense.” It is time for her to move up to the next level.

eactions and the Math Behind the Column

Ezra Klein: Given his 780,386 Twitter followers, a tweet from Ezra Klein is worth reporting. I like his modification to my tweet: 

No, she’s a human being RT @mileskimball: Don’t miss my column “Janet Yellen is hardly a dove”http://blog.supplysideliberal.com/post/63725670856/janet-yellen-efficiency-wages-and-monetary-policy

Andy Harless’s Question: Where Does the Curvature Come From? Andy Harless asks why there is an asymmetry—in this case a curvature—that makes things different when unemployment goes up than when it goes down. The technical answer is in Carl Shapiro and Joseph Stiglitz’ paper “Unemployment as a Worker Discipline Device.” It is not easy to make this result fully intuitive. A key point is that unemployed folks find jobs again at a certain rate. This and the rate at which diligent workers leave their jobs for exogenous reasons dilute the motivation from trying to reduce one’s chances of leaving a job. The discount rate r also dilutes any threats that get realized in the future. So the key equation is 

dollar cost of effort per unit time 

                    =  (wage - unemployment benefit) 

                                                          · detection rate

÷ [detection rate + rate at which diligent workers leave their jobs                              + rate at which the unemployed find jobs + r]  

That is, the extra pay people get from work only helps deter dereliction of duty according to the fraction of the sum of all the rates that comes from the detection probability. And the job finding rate depends on the reciprocal of the unemployment rate. So as unemployment gets low, the job finding rate seriously dilutes the effect of the detection probability times the extra that workers get paid.

(The derivation of the equation above uses the rules for dealing with fractions quite heavily, backing up the idea in the WSJ article I tweeted as follows.

The Dividing Line: Why Are Fractions Key to Future Math Success?http://on.wsj.com/15rlupS

Deeper intuition for the equation above would require developing a deeper and more solid intuition about fractions in general than I currently have.)

Solving for the extra pay needed to motivate workers yields this equation:

(wage - unemployment benefit) 

           = dollar cost of effort per unit time 

· [detection rate + rate at which diligent workers leave their jobs                              + rate at which the unemployed find jobs + r]  ÷

                                  detection rate

In labor market dynamics the rates are high, so a flow-in-flow-out steady state is reached fairly quickly, and we can find the rate at which the unemployed find jobs by the equation flow in = flow out, or since in equilibrium the firms keep all their workers motivated,  

rate at which diligent workers lose jobs * number employed

= rate at which the unemployed find jobs * number unemployed.

Solving for the rate of job finding:

rate at which the unemployed find jobs 

= rate at which diligent workers leave their jobs 

· number employed  ÷  number unemployed

Finally, it is worth noting that

rate at which diligent workers leave their jobs

+ rate at which the unemployed find jobs

= rate at which diligent workers leave their jobs 

· [number unemployed + number employed]/[number unemployed]

= rate at which diligent workers leave their jobs 

÷ unemployment rate

Morgan Warstler’s Reply: The original link in the column about Morgan Warstler’s plan was to a Modeled Behavior discussion of his plan. Here is a link to Morgan Warstler’s own post about his plan. Morgan’s reply in the comment thread is important enough I will copy it out here so you don’t miss it:

1. The plan is not Dickensian. It allows the poor to earn $280 per week for ANY job they can find someone to pay them $40 per week to do. And it gives them the online tools to market themselves.

Work with wood? Those custom made rabbit hatches you wish you could get the business of the ground on? Here ya go.

Painter, musician, rabbit farmer, mechanic - dream job time.

My plan is built to be politically WORKABLE. The Congressional Black Caucus, the Tea Party and the OWS crowd. They are beneficiaries here.

2. No one in economics notices the other key benefit - the cost of goods and services in poor zip codes goes down ;:So the $280 minimum GI check buys 30% more! (conservative by my napkin math) So real consumption goes up A LOT.

This is key, bc the effect is a steep drop in income inequality, and mobility.

That $20 gourmet hamburger in the ghetto costs $5, and it’s kicking McDonalds ass. And lots of hipsters are noticing that the best deals, on things OTHER THAN HOUSING are where the poor live.

Anyway, I wish amongst the better economists there was more mechanistic thinking about how thigns really work.

How the Idea that Intelligence is Genetic Distorted My Life—Even Though I Worked Hard Trying to Get Smarter Anyway

Miles in Copenhagen, September 2013

Miles in Copenhagen, September 2013

The idea that intelligence is inborn makes us less intelligent by discouraging effort. It also distorts our lives in other ways. I wanted to share my story–a story Noah Smith and I couldn’t figure out how to fit into our column “Power of Myth: There’s one key difference between kids who excel at math and those who don’t.” Here is my story. Along the way, you will see how competitive I am. I hope you don’t come to hate me too much as a result!

For most of my life, I believed firmly in the idea that intelligence was mostly genetic, and much of my identity was wrapped up in “being the smartest kid on the block”—with as big a “block” as possible. But, I knew I couldn’t convince others of how smart I was without working hard in some sense. The trick to convincing both myself and others of my intelligence was to work hard in ways that were off the books. Working hard in a class I was actually in: not cool. Browsing in the math section of a nearby university library, honing public speaking skills on the debate team, reading the encyclopedia, reading Isaac Asimov’s science and history books, and reading the New York Times and the Wall Street Journal: cool. Listening to the teacher with both ears: not cool. Double-tasking by inventing a new game or fiddling with mathematical equations while the English teacher was talking and still doing my best to dominate the class discussion: cool. To avoid feeling I was just a grind, working hard like the peons obsessed by getting good grades, I always tried to find a bigger game to play, like learning things that would help once I got to college rather than learning things for my high school classes.

Once I actually got to college, with many other smart competitors, I knew I would have to work hard in ways more directly related to classes. But the desire to impress my classmates with the appearance of little input for high performance was still there. I still get a frisson of joy remembering the time one of my classmates expressed awe that I managed to survive in college despite not studying on Sunday. What he didn’t realize was that–in terms of time available for studying–my religious strictures against drinking and carousing more than made up for my rule against studying on Sunday.

What I hope you get from the story so far is not the fact that I must have seemed insufferable, but this: one way or another, I figured out ways to work very hard while never seeming to work hard. I fooled even myself, at least in part, especially by routinely working hard on things other than what I was supposed to be working on at the moment.

Despite having a strategy that spared me the worst excesses of smart-kid laziness, the idea that being innately smart was what counted rather than hard work caused me a lot of psychic pain along the way. There came a point in my career when I wondered why other economists were passing me by in prestige and honors. At long last I realized that being a successful economist isn’t just about proving one is smart. The currency of the realm is writing academic papers and shepherding them through endless rounds of revision to get them published in academic journals. There is a limit to how much of my time I am willing to spend on that activity. So this realization alone did not rocket me to the top of the profession. But at least I understand what is going on. Hard work is needed not only in order to get smarter, but also to get the payoff from being smart–whatever type of payoff I choose to pursue.

Quartz #33—>Don't Believe Anyone Who Claims to Understand the Economics of Obamacare

Link to the Column on Quartz

Here is the full text of my 33d Quartz column “Don’t believe anyone who claims to understand the economics of Obamacare,“ now brought home to supplysideliberal.com. It was first published on October 3, 2013. Links to all my other columns can be found here.

If you want to mirror the content of this post on another site, that is possible for a limited time if you read the legal notice at this link and include both a link to the original Quartz column and the following copyright notice:

© October 3, 2013: Miles Kimball, as first published on Quartz. Used by permission according to a temporary nonexclusive license expiring June 30, 2015. All rights reserved.

Below, after the text of the column as it appeared in Quartz, I have the original introduction, and some reactions to the column.  

Republican hatred of Obamacare and Democratic support for Obamacare have shut down the US government. Now might be a good time to remind the world just how far the country’s health care sector—with or without Obamacare—is from being the kind of classical free market Adam Smith was describing when he talked about the beneficent “invisible hand” of the free market. There are at least five big departures of our health care system from a classical free market:

1. Health care is complex, and its outcomes often cannot be seen until years later, when many other confounding forces have intervened.  So the assumption that people are typically well informed—or as well informed as their health care providers—is sadly false. (And the difficulties that juries have in understanding medicine create opportunities for lawyers to get large judgments for plaintiffs in malpractice suits.)

2. Even aside from the desire to cure contagious diseases before they spread, people care not only about their own health and the health of their families, but also the health of strangers. On average, it makes people feel worse to see others suffering from sickness than to see others suffering from aspects of poverty unrelated to sickness.

3. “Scope of practice” laws put severe restrictions on what health care workers can do. For example, there are many routine things that nurses could do just as well as a general practitioner, but are not allowed to do because they are not doctors–and the paths to becoming a “medical doctor” are strictly controlled.

4. Those who have insurance pay only a small fraction of the cost of the medical procedures they get, leading them to agree to many expensive medical procedures even in cases where the benefit is likely to be small.

5. In order to spur research into new drugs, the government gives temporary monopolies on the production of life-saving drugs—a.k.a. patents—that push the price of those drugs far above the actual cost of production. 

Sometimes these departures from a classical free market cancel each other out, as when insurance firms shield patients from the official price of a drug and make the cost of that drug to the patient close to the social cost of producing it, or when laws prevent outright quacks from performing brain surgery on an ill-informed patient. But one way or another, there is no obvious “free market” anywhere in sight. That doesn’t mean that the economic reasoning behind the virtues of the free market doesn’t help, it just means that when we think about health care policy, we swim in deep water.

At the level of overall health care systems, one of the most important things we know is that many other countries seem to get reasonably good health care outcomes while spending much less money than we do in the US. There are several factors that might contribute to relatively good health results in other countries:

  • There are large gains in health from making sure that everyone in society gets very basic medical care on a basis more regular than emergency room visits.
  • Most other countries have less of a devotion to fast food—and food from grocery store shelves that is processed to taste as good as possible (in the sense of “can’t eat just one”) without regard to overall actual (as opposed to advertising-driven) health properties.
  • Most other countries are either poor enough, or rely enough on public transportation, that people are forced to walk or ride bicycles significant distances to get to where they need to go every day.

Part of the recipe for spending less in other countries is the fact that they can cheaply copy drugs and medical techniques developed in the US at great expense, But, there are two simple ingredients to the recipe beyond that:

  • Ration procedures that don’t seem very effective (inevitably along with some inappropriate rationing as well)
  • Use the fact that most of the money for health care runs through the government as leverage to push down the pay of doctors and other health care workers.

My main concern about Obamacare is the fear that it will inhibit experimentation with different ways of organizing health care at the state level. So far that is only a fear, but it is something to watch for. But there is one way in which state-level approaches are severely limited: they can’t push down the pay of doctors and other health care workers without causing an exodus of doctors and other health care workers to other states. National health care reform can be more powerful than state-level health care reform if a key aim, stated or not, is to reduce the pay of doctors and other health care workers (and workers in closely connected fields, such as those who work in insurance companies) in order to make medical care cheaper for everyone else. Fewer stars would go into medicine if it paid less—but if most of the benefits from health care are from basic care, that might not show up too much in the overall health statistics. And if less-expensive nurses can do things that expensive doctors are now doing, those who would have been nurses will still do a good job if they end up becoming doctors because the pay is too low for the stars to fill the medical school slots.

Reducing the total amount of money flowing through the health care sector should reduce both the amount of health care and the price of health care. But even in a best-case scenario, in which reasonably judicious approaches to rationing and dramatic advances in persuading people to exercise and eat right kept the overall health statistics looking good, a reduction in the price and quantity of health care could mean a big reduction in income for those working in health care and related fields.

Still, the key wild card in judging Obamacare will be its effect on health care innovation. Subsidies may get people more care now, but crowd out government funding for basic medical research. Efforts to standardize medical care could easily yield big gains at the start as hospitals come up to best practice, yet that standardization could make innovation harder later on. An emphasis on cost-containment could encourage cost-reducing innovations, but discourage the development of new treatments that are very expensive at first, but could become cheaper later on. And Obamacare will tend to substitute the judgments of other types of health care experts in place of the judgments of business people, with unknown effects. Whatever the effects of Obamacare on innovation, we can be confident that over time these effects on innovation will dwarf most of the other effects of Obamacare in importance.

The October 2013 US government shutdown is only the latest of many twists and turns in the bitter struggle over Obamacare. A large share of the partisan energy comes from people who feel certain they know what Obamacare will do. But ideology makes things seem obvious that are not obvious at all. The social science research I have seen on health care regularly turns up surprises. To me, the most surprising thing would be if what Obamacare actually does to health care in America didn’t surprise us many times over, both pleasantly and unpleasantly, at the same time.

Here is my original introduction, which was drastically trimmed down for the version on Quartz: 

Republican hatred of Obamacare, and Democratic support for Obamacare, have shut down the “non-essential” activities of the Federal Government. So, three-and-a-half years since President Obama signed the “Patient Protection and Affordable Care Act” into law, and a year or so since a presidential election in which Obamacare was a major issue, it is a good time to think about Obamacare again.

In my first blog post about health care, back in June 2012, I wrote:

I am slow to post about health care because I don’t know the answers. But then I don’t think anyone knows the answers. There are many excellent ideas for trying to improve health care, but we just don’t know how different changes will work in practice at the level of entire health care systems.  

That remains true, but thanks to the intervening year, I have high hopes that with some effort, we can be, as the saying goes, “confused on a higher level and about more important things.”

One thing that has come home to me in the past year is just how far the US health care sector—with or without Obamacare—is from being the kind of classical free market Adam Smith was describing when he talked about the beneficent “invisible hand” of the free market. 

Reactions: Gerald Seib and David Wessel Included this column in their “What We’re Reading” Feature in the Wall Street Journal. Here is their excellent summary:

The key to the long-run impact of Obamacare will be whether it smothers innovation in health care — both in the way it is organized and in the development of new treatments. And no one today can know whether that’ll happen, says economist Miles Kimball. [Quartz]

(In response, Noah Smith had this to say about me and the Wall Street Journal.) This column was also featured in Walter Russell Mead’s post "How Will We Know If Obamacare Succeeds or Fails.” (Thanks to Robert Graboyes for pointing me to that post.) He writes:

Meanwhile, at Quartz, Miles Kimball has a post entitled “Don’t Believe Anyone Who Claims to Understand the Economics of Obamacare.” The whole post is worth reading, but near the end, he argues that the ACA’s effect on innovation could eventually be the most important thing about it’s long-term legacy…

From our perspective, these are both very good places to start thinking about how to measure Obamacare’s impact. Of course, Tozzi’s metric is easier to quantify than Kimball’s: it will be difficult to judge how the ACA is or isn’t limiting innovation. But that doesn’t mean we shouldn’t try: without innovation, there’s no hope for a sustainable solution to the ongoing crisis of exploding health care costs.

I have also been pleased by some favorable tweets. Here is a sampling:

Ben Bernanke: The Fed Does Less Monetary Stimulus Than It Thinks Is Warranted Because It Is Afraid of the Side Effects of Unconventional Tools

On January 14, 2013, Ben Bernanke came to a Q&A session at the University of Michigan, sponsored by the Ford School of Public Policy. Here is the video and the full transcript can be found here. I thought Ben said some particularly important things about the use of unconventional tools of monetary policy and about financial stability. Let me excerpt four question and answer exchanges. I consider the last of the four the most important.

The Effectiveness of Quantitative Easing

Susan Collins (Dean of the Ford School): …the Fed, of course, has been keeping interest rates at close to zero since roughly 2008. And it’s dug pretty deep into its arsenal and very unconventional policies more recently in terms of, in particular, the very massive asset purchases recently launched its third round which are intended to bring long-term interest rates. Can you tell us how well you think that is working?

Ben Bernanke: So, to go back just one step, as you said, we’ve brought the short-term interest rate down almost to zero. And for many, many years, monetary policy just involved moving the short-term, basically, overnight interest rate up and down and hoping that the rest of the interest rates would move in sympathy. Then we hit a situation in 2008 where we had brought the short-term rate down about as far as it could go, almost entirely to zero. And so, the question is, what more could the Fed do? And there were many people–a decade ago, there were a lot of articles about how the Fed would be out of ammunition if they got the short-term rate down to zero. But a lot of work by academics and others, researchers at the central banks suggested there was more that could be done once you got the short-term rate down to zero. And in particular, what you could do is try to address the longer term interest rate, bring longer term rates down. And there are two basic ways to do that. One way is through talk, communication, sometimes called open mouth operations. [Laughter] The idea being that if you tell the public that you’re going to keep rates low in the long-term, that that will have the effect of pushing down longer term interest rates. But the quest–the one you’re asking about is what we call at the Fed large scale asset purchases or otherwise known as QE. The idea there is that by buying large quantities of longer term treasury securities or mortgage-backed security so that we can drive down interest rates on those key securities. And that, in turn, affects spending investment in the economy. The latest episode, you know, so far, we think we are getting some effect. It’s kind of early. But overall, it’s clear that through the three iterations that you refer to that we have succeeded in bringing longer-term rates down pretty significantly, and a clear evidence of that would be mortgage rates, as you know, a 30-year mortgage rate is something like 3.4 percent now, incredibly low. And that, in turn, makes housing very affordable. And that, in turn, is helping the housing sector recover, creating construction jobs, raising house prices, increasing activity in that sector, real estate activity, and so on. So, I think broadly speaking, that we have found this to be an effective tool. But we’re going to continue to assess how effective, because it’s possible that as you move through time and the situation changes that the impact of these tools could vary. But I think what we have decisively shown is that the short-term interest rate getting down to zero, but economists call it the zero lower bound problem, it does not mean the Fed is out of ammunition. There are still things we can do, things we have done. And I would add that other central banks around the world had done similar things and have also had some success in creating more monetary policy support for the economy….

Inflation and Financial Stability Risks of Fed Stimulus

Susan Collins: And I wonder what you might say to those who argue that … the massive asset purchases have created extremely high risks, perhaps, under appreciated risks for future inflation.

Ben Bernanke: …the Federal Reserve has a dual mandate from the Congress to achieve or at least to try to achieve price stability and maximum employment. Price stability means low inflation. We have basically taken that to be two percent inflation. Inflation has been very low. It’s been below two percent and appears to be on track to stay below two percent. So, our price stability record is very good. Unemployment, though, as we’ve already discussed, is still quite high. It’s been coming down but very slowly. And the cost of that is enormous in terms of lost, you know, lost resources, hardship, talents and skills being wasted. So, our effort to try to create more strength in the economy, to try and put more people back to work, I think that’s an extraordinarily important thing for us to be doing. And I think it motivates and justifies what has been, I agree, an aggressive monetary policy. So, that’s what we’re doing and that’s why we’re doing it. Now, are there downsides? Are there potential costs and risks? There are some. You mentioned inflation. We have, obviously, used very expansionary monetary policy. We’ve increased the monetary base which is demand reserves that banks hold with the Fed. There are some people who, I think, that’s going to be inflationary. Personally, I don’t see much evidence in that. Inflation, as I’ve mentioned has been quite flow. Inflation expectations remain quite well-anchored. Private sector forecasters do not see any inflation coming up. And in particular, we have, I believe, we have all the tools we need to undo our monetary policy stimulus and to just–to take that away before inflation becomes our problem. So, I don’t believe that significant inflation is going to be a result of any of this. That being said, price stability is one part of our tool mandate, and we will be paying very close attention to make sure that inflation stays well contained as it is today. A second issue, I think, probably worth mentioning is financial stability. This is a difficult issue. The concern is–has been raised at–by keeping interest rates very low, that we induce–the Federal Reserve induces people to take greater risks in their financial investments, and that, in turn, could lead to instability later on, again, a difficult question. In fact, I could take the rest of the hour talking about this, so I don’t think I’ll do that. But what I will say is that we are, first of all, very engaged in monitoring the economy, the financial system. The Fed has increased enormously the amount of resources we put into monitoring financial conditions and trying to understand what’s happening in different sectors of the financial markets. We’ve also, of course, been part of the very extended effort to strengthen our financial system by increasing capital in banks, by making derivatives and transactions more transparent, by stiffening supervision, and so on. So, we are taking measures to try both to prevent financial instability and to identify potential risks that we would then address through regulatory or supervisory methods. So, we’re very much attuned those–to these issues. But once again, I think this is something that we need to pay careful attention to. And as I–as we discussed in our statement and have for a while, as we evaluate these policies, we’re going to be looking at the benefits which, I believe, involve some help to economic growth to reduction in unemployment. But we’re also going to be looking at cost and risk. We have a cost benefit type of approach here. We want to make sure that the actions we’re taking are fully justified in a cost benefit type of framework. …interest rates will eventually rise. We hope they rise, because that means the economy will be strengthening. So, you know, we’re not going to playing games with that. We are going to follow our mandate, which means do what’s necessary to help the economy be strong. … Indeed, I think the worst thing we could do would be if we raise interest rates prematurely and caused recession, that would greatly increase budget deficits.

Monetary vs. Regulatory Approaches to Financial Stability

Audience Question: Do you believe that the Fed should actively prevent future asset bubbles and if so what tools do you have to do that?

Ben Bernanke: Well, asset bubbles have been–they’re very, very difficult to anticipate, obviously. But we can do some things. First of all, we can try to strengthen our financial system, say, by increase–as I mentioned earlier, by increasing the amount of capital liquidity the banks hold, by improving the supervision of those banks, by making sure that every important financial institution is supervised by somebody. There were some very important ones during the crisis that essentially had no effective supervision. So you make the system stronger that if a bubble or some other financial problem emerges, the system will be better able to be more resilient, will be better able to survive the problem. Now, you can try to identify bubbles and I think there has been a lot of research on that, a lot of thinking about that. We have created a council called the Financial Stability Oversight Council, the FSOC, which is made up of 10 regulators and chaired by the Secretary of the Treasury. One of whose responsibilities is to monitor the financial system as the Fed also does and try to identify problems that emerge. So, you’re not going to identify every possible problem for sure but you can do your best and you can try to make sure that the system is strong. And when you identify problems, you can use–I think the first line of defense needs to be regulatory and supervisory authorities that not only the Fed but other organizations like the OCC and the FDIC and so on have as well. So you can address these problems using regulatory and supervisory authorities. Now having said all that, as I was saying earlier, there’s a lot of disagreement about what role monetary policy plays in creating asset bubbles. It is not a settled issue. There are some people who think that it’s an important source of asset bubbles, others would think, it’s not. Our attitude is, that we need to be open-minded about it and to pay close attention to what’s happening and to the extent that we can identify problems. You know, we need to address that. The Federal Reserve was created in about 100 years ago now, 1930 was the law, not to do monetary policy but rather to address financial panics. And that’s what we did, of course, in 2008 and 2009. And it’s a difficult task but I think going forward, the Fed needs to think about financial stability and monetary economics stability as being, in some sense, the two key pillars of what the Central Bank tries to do. And so we will, obviously, be working very hard in financial stability. We’ll be using our regulatory and supervisory powers. We’ll try to strengthen the financial system. And if necessary, we will adjust monetary policy as well but I don’t think that’s the first line of defense.

Costs and Benefits of Unconventional Tools of Monetary Policy

Question Tweeted In: This question comes from Twitter. Since the Fed declared it was targeting a two percent inflation rate in January of 2012, the FOMC has released its projections five times. And each one of these projections, the inflation rate has come in below this target. Why then has the policy been set to concessively undershoot the target?

Ben Bernanke: Was that 140 characters? [ Laughter ] I suspect many in our audience had related questions. [Laughter] Yeah. That’s a very good–it’s a very good question and let me try to address. As I said earlier when Dean Collins was asking me about the risks of some of our policies, I was pointing out that inflation is very low. Indeed, it’s below the two percent target and unemployment is above where it should be and therefore, there seems to be a pretty strong presumption that we should be aggressive in monetary policy. So, you know, I think that that does make the case for being aggressive which we are trying to do. Now, the additional point that I made, though, was that, you know, the short-term interest rate is close to zero and therefore we are now in the world of non-standard monetary policy [inaudible] asset purchases and communications and so on. And as we were discussing earlier, we have to pay very close attention to the costs and the risks and the efficacy of these non-standard policies as well as the potential economic benefits. And to the extent that there are costs or risks associated with non-standard policies which do not appear or at least not to the same degree for standard policies then you would, you know, economics tells you when something is more costly, you do a little bit less of it. We are being quite accommodative. We are working very hard to try to strengthen the economy. Inflation is very close to the target. It’s not radically far from the target. But in trying to think about what the right policy is, we have to think not only about the macroeconomic outlook which is obviously very critical, but also the costs and risks associated with the individual policies that we might apply.

The Red Banker on Supply-Side Liberalism

Icon for the Red Banker blog (which also appears in Wikipedia article on the “Commercial Revolution”)

Icon for the Red Banker blog (which also appears in Wikipedia article on the “Commercial Revolution”)

Frederic Mari blogs as the Red Banker. He gives a positive take on my first post “What is a Supply-Side Liberal?” in his post “Supply Side Liberalism: The Interesting Case of Dr. Kimball and Mr. Miles.” However, Frederic questions whether limited government is politically possible, saying

People oppose government spending but support all of its public good provision.

Here I wished he had discussed my central proposal for keeping the burden of taxation down while providing abundant public goods: a public contribution system that raises taxes rates, but lets people avoid 100% of the extra taxes by making charitable donations focused on doing things the government might otherwise have to do. These two posts lay out how a public contribution system would work: 

Also, my post 

is best understood in this context.

I discuss a few other ideas for how to reduce the burden of taxation based on the ways in which human psychology departs from over-simplified views of homo economicus in this popular post: 

The bottom line is this: In my book, it isn’t Supply-Side Liberalism without a serious effort to lower the burden of taxation for any given level of revenue, using everything we know about human nature.

The Unavoidability of Faith

Sometimes we think of faith as something optional, and something directed toward the supernatural. Not so. Faith is unavoidable, and faith directed toward the supernatural is a small part of all faith.

As for many discussions of faith, the starting point for my discussion of faith are the words of the (unknown) author of the Epistle to the Hebrews. Using William Tyndale’s translation with modern spelling, Hebrews 11:1 reads

Faith is a sure confidence of things which are hoped for and a certainty of things which are not seen. 

In my book, the more evidence we have to go on and the less faith we have to depend on, the better. That is, I disagree with the words the resurrected Jesus is reported to have said to a doubting Thomas (John 20:29, Tyndale):

Thomas, because thou hast seen me therefore thou believest: Happy are they that have not seen and yet believe.

Rather, happy are they who have much evidence to base their choices on. But choices–to act, or not to act–often have to be made when evidence is scarce. That is where faith comes in.

One might be tempted to think of faith as a Bayesian prior. But it isn’t that simple. In Bayesian decision-making, “prior beliefs” are left unexplained. But in the real world they come from different ways of responding to and reasoning about past experience. New data sometimes simply updates prior beliefs within the same paradigm, as Bayesian theory suggests. But other times, new data upends the thin tissue of reasoning and reaction that was crucial for the formation of those prior beliefs, resulting in a much bigger change in views than straightforward Bayesian updating would imply. And sometimes additional reasoning–in the absence of any additional data whatsoever–can dramatically change one’s views.

A simpler point is that what is prior to one set of events is posterior to earlier events. Putting both points together, faith is what one believes at a given moment in time, however one has managed to cobble together those beliefs.

In situations where one is willing to think of one choice as inaction, with costly actions having debatable benefits, one can distinguish between a “belief in nothing” that leads one to continue in inaction, and a “belief in something” that leads one to act. When proponents of action say “Have faith!” they are advocating a belief in a high enough marginal product of action to make it worth the costs. That is very much the perspective of the Lectures on Faith, which were once part of the Mormon canon, but now enjoy only semi-canonical status. (The full text of the Lectures on Faith can be found here.)  Let me quote a passage from the Lectures on Faith that has stuck with me, again modernizing the spelling:    

If men were duly to consider themselves, and turn their thoughts and reflections to the operations of their own minds, they would readily discover that it is faith, and faith only, which is the moving cause of all action, in them; that without it, both mind and body would be in a state of inactivity, and all their exertions would cease, both physical and mental.

Were this class to go back and reflect upon the history of their lives, from the period of their first recollection, and ask themselves, what principle excited them to action, or what gave them energy and activity, in all their lawful avocations, callings and pursuits, what would be the answer? Would it not be that it was the assurance which we had of the existence of things which we had not seen, as yet? Was it not the hope which you had, in consequence of your belief in the existence of unseen things, which stimulated you to action and exertion, in order to obtain them? Are you not dependent on your faith, or belief, for the acquisition of all knowledge, wisdom and intelligence? Would you exert yourselves to obtain wisdom and intelligence, unless you did believe that you could obtain them? Would you have ever sown if you had not believed that you would reap? Would you have ever planted if you had not believed that you would gather? Would you have ever asked unless you had believed that you would receive? Would you have ever sought unless you had believed that you would have found? Or would you have ever knocked unless you had believed that it would have been opened unto you? In a word, is there any thing that you would have done, either physical or mental, if you had not previously believed? Are not all your exertions, of every kind, dependent on your faith? Or may we not ask, what have you, or what do you possess, which you have not obtained by reason of your faith? Your food, your raiment, your lodgings, are they not all by reason of your faith? Reflect, and ask yourselves, if these things are not so. Turn your thoughts on your own minds, and see if faith is not the moving cause of all action in yourselves; and if the moving cause in you, it it not in all other intelligent beings?

Application 1: The Cognitive Economics of Human Capital

Let me apply this idea to Jill’s decision of whether to go to college and learn economics or not. Some consequences of college might be relatively easy to discern, such as the costs,  and if she is relatively well informed, the likely effect on her future wage. But what about the benefits learning economic analysis might have for her future decision-making? A tempting approach to analyzing Jill’s problem would be to think of her computing what her life would be like (or a probability distribution thereof) if she does go to college, as well as what her life would be like if she doesn’t go to college, compare the two to see which one she prefers, and make that choice. But in this case, Jill can't compute what her life will be like if she goes to college and learns economics because she doesn’t know now the analytical tools that could influence her life in critical ways if she does go to college and learn economics. In other words, she can’t make a fully rational choice (according to the demanding standards of most economic models) of whether or not to go to college without knowing the very things that she would be learning in college. But if she knew those things already, she wouldn’t need to go to college!  

The Handbook of Contemporary Behavioral Economics: Foundations and Developments, page 343 points to the more general conundrum of which Jill’s problem is an example:

The inability to formulate an optimization problem that folds in the cost of its own solution has become known as the “infinite regress problem,” with Savage (1954) appearing to be the first to use the regress label.  

Application 2: The Cognitive Economics of R&D

Another good example of the infinite regress problem is the decision of which lines of research to pursue. The issue is stark in a decision of whether or not to undertake a research project in mathematical economic theory. There is no way to make a fully rational decision according to the demanding standards of most economic models because the most economic models assume that information processing (as distinct from information acquisition) comes free, but the issue is precisely whether one’s own finite thinking ability will allow one to find a publishable theoretical result within a reasonable amount of time. Therefore, one must make the decision according to a hunch of some sort–or in other words, by faith. The analogy that makes one believe that a proof might exist is not itself the proof, and may fall apart. But that analogy makes one willing to take the risk. Except in cases where undecidability of the sort that shows up in Goedel’s theorem comes into play, the only fully rational probability that one could find a proof would be either 0 or 1, because one would already know the answer. But that just isn’t the way it is when you make the decision. You have some notion of the probability you will be able to find a proof–a probability that by its nature cannot have a firm foundation, yet still guides one’s choice: faith.

Application 3: The Cognitive Economics of Economic Growth

Growth theory faces a similar problem. It would be a lot easier to form a sensible probability distribution for future technological progress if one actually knew the technology already. Someday, economists studying the economics of other planets under the restriction of Star Trek’s (often violated) Prime Directive of non-intervention may be able to do growth theory that way. But we 21st century economists must do growth theory in ignorance of scientific and engineering principles that may be crucial to future economic growth. It would be nice to know the answers to questions such as how hard it is to make batteries more efficient, for example, or whether theoretically possible subatomic particles that could catalyze fusion exist or not. (My friend, theoretical physicist James Wells, has worked on the theory. The right kind of heavy, but relatively stable negatively charged particle could do it by taking the place of electrons in hydrogen atoms and making the exotic hydrogen atoms much smaller in size.) If it were all just a matter of getting experimental results, the economic model might be standard, but what if just thinking more clearly with the evidence one already has could make it possible to get to the answer with one decisive experiment instead of an inefficient series of 100 experiments. 

Just as with the standard approach to human capital, we often look at technological progress from the outside, in a relatively bloodless way: a shifter in the production function changes. But the inside story of most technological progress is that in some sense we were doing something stupid, but now have stopped being stupid in that particular way. I say “in some sense” because–while our finite cognition is painful–it is possible to be smart in recognizing our cognitive limitations and making reasonable decisions despite having to walk more by faith that we would like in making decisions that depend on technologies we don’t yet know exist.

Application 4: Locus of Control

A central life decision is whether to attempt to better one’s life by making an effort to do so. Information acquisition and learning how to process information are themselves costly, so the initial decision of whether to do the information acquisition and other learning that are a logical first step must be made in a fog of ignorance. Some people are lucky enough to have parents who instill in them confidence that effort to gain knowledge, learn and grow will be well rewarded in life, at least on average. It is good luck to have that belief, because it seems to be true for most people. But believing that it is true for you–that your efforts to better your life will be rewarded–must be an act of faith. For you are not exactly like anyone else. And even knowing that most people are similar in this regard is a bit of knowledge that might cost you dearly to acquire if you are not so lucky to as to have your parents, or someone else you trust tell you so.

If you decide that it is not worth the effort trying to better your life, you will not collect much evidence on the marginal product of effort, and so there will be precious little that could provide direct evidence to change your mind. In such a low-effort trap, it will not be hard evidence about your own marginal product of effort that switches you from believing in an external locus of control (outside forces govern outcomes with little effect of own effort) to an internal locus of control (own efforts have an important effect on quality of outcomes). If you escape the trap of believing in an external locus of control, it will be by believing some kind of evidence or reasoning that is much less definitive.

Conclusion

I do not believe in the supernatural. So for me, faith is not about the supernatural. Yet still we must walk by faith. Walking by the light of evidence is better, but such is not always our lot.

Not only must we sometimes walk by faith–whether we like or not–so must others. It matters what kind of faith we instill in those around us, to the extent we have any influence.

To me, faith in progress and human improvability–both individually and collectively–is a precious boon. It is not enough for us to have that faith. Many are caught in what I believe to be the trap of believing they can not better their lives. I believe it is important for them to have faith in progress and human improvability as well. If you believe in progress and human improvability as I do, let us together seek for better and better ways of transmitting that faith to those who do not yet believe.

Monetary vs. Fiscal Policy: Expansionary Monetary Policy Does Not Raise the Budget Deficit

Monetary policy and fiscal policy are not equally good as ways to stimulate the economy. Traditional monetary policy (that is, lowering the short-term interest rate) has two key advantages over traditional fiscal policy:

  • It does not add to the national debt
  • Because many governments have–however controversially–been willing to let monetary policy be handled by an independent central bank, it is not doomed to be tangled up in politics to the same extent that discretionary fiscal policy inevitably gets tangled up in long-running political disputes about taxing and spending.

My subtitle “Expansionary Monetary Policy Does Not Raise the Budget Deficit” is a quotation from Alan Blinder’s October 25, 2010 Wall Street Journal op-ed “Our Fiscal Policy Paradox,” where Alan also points to the political difficulties of using discretionary fiscal for macroeconomic stabilization:

The practice of monetary and fiscal policy is fraught with difficulties, but the central concept is straightforward, compelling and, by the way, 75 years old: The government should push the economy forward when unemployment is high and slow it down when inflation threatens.
To do so, governments normally have two principal sets of weapons. Fiscal policy means moving some taxes or elements of public spending up or down to either propel or restrain total spending. In the United States, such decisions are made politically, by Congress and the president. Monetary policy normally (but not now) means lowering or raising short-term interest rates to either speed up growth or slow it down. That power, of course, resides in the technocratic Federal Reserve….
There are plenty of powerful weapons left in the fiscal-policy arsenal. But Congress is tied up in partisan knots that will probably get worse after the election….
But what about using monetary policy? Chairman Ben Bernanke and his Federal Reserve colleagues are not paralyzed by politics. They have not fallen victim to misleading advertising claiming that past policies have not helped. And expansionary monetary policy does not raise the budget deficit. So why the hesitation?

Monetary Policy. My view is that we need tools for macroeconomic stabilization that (a) can be applied technocratically and (b) do not add greatly to national debt when they are used to stimulate the economy. Monetary policy fills that bill, once it is unhobbled by eliminating the zero lower bound. Here is what I wrote in my column “Why Austerity Budgets Won’t Save Your Economy”:

For the US, the most important point is that using monetary policy to stimulate the economy does not add to the national debt and that even when interest rates are near zero, the full effectiveness of monetary policy can be restored if we are willing to make a legal distinction between paper currency and electronic money in bank accounts—treating electronic money as the real thing, and putting paper currency in a subordinate role….
Without the limitations on monetary policy that come from our current paper currency policy, the Fed could lower interest rates enough (even into negative territory for a few quarters if necessary) to offset the effects of even major tax increases and government spending cuts.

The Costs of National Debt. That column is also important in giving some of the best arguments I know for worrying about the national debt now that it is hard to argue that national debt slows economic growth. (On the effect of national debt on economic growth, see my two columns with Yichuan Wang “After Crunching Reinhart and Rogoff’s Data, We Found No Evidence High Debt Slows Growth” and Examining the Entrails: Is There Any Evidence for an Effect of Debt on Growth in the Reinhart and Rogoff Data? and the other work they flag.) Here is what I had to say about the costs of debt in "Why Austerity Budgets Won’t Save Your Economy“:

…lenders are showing no signs of doubting the ability of the US government to pay its debts. But there can be costs to debt even if no one ever doubts that the US government can pay it back.
To understand the other costs of debt, think of an individual going into debt. There are many appropriate reasons to take on debt, despite the burden of paying off the debt:
  • To deal with an emergency—such as unexpected medical expenses—when it was impossible to be prepared by saving in advance.
  • To invest in an education or tools needed for a better job.
  • To buy an affordable house or car that will provide benefits for many years.
There is one more logically coherent reason to take on debt—logically coherent but seldom seen in the real world:
  • To be able to say with contentment and satisfaction in one’s impoverished old age, “What fun I had when I was young!”
In theory, this could happen if when young, one had a unique opportunity for a wonderful experience—an opportunity that is very rare, worth sacrificing for later on. Another way it could happen is if one simply cared more in general about what happened in one’s youth than about what happened in one’s old age.
Tax increases and government spending cuts are painful. Running up the national debt concentrates and intensifies that pain in the future. Since our budget deficits are not giving us a uniquely wonderful experience now, to justify running up debt, that debt should be either (i) necessary to avoid great pain now, or (ii) necessary to make the future better in a big enough way to make up for the extra debt burden. The idea that running up debt is the only way to stimulate an economic recovery when interest rates are near zero is exactly what I question… If reforming the way we handle paper currency made it clear that running up the debt is not necessary to stimulate the economy, what else could justify increasing our national debt? In that case, only true investments in the future would justify more debt: things like roads, bridges, and scientific knowledge that would still be there in the future yielding benefits—benefits for which our children and we ourselves in the future will be glad to shoulder the burden of debt.

National Lines of Credit: I write about the importance of stabilization policy that can be applied technocratically, without getting tangled up in politics in the context of my other main proposal for stabilization policy: National Lines of Credit (or equivalently "Federal Lines of Credit”). The key post there is “Preventing Recession-Fighting from Becoming a Political Football.” In any case, I think National Lines of Credit would get less tangled up in politics than regular traditional fiscal policy, but it would also be possible to set them up so that they were initiated in an explicitly technocratic way. Here is the relevant passage from my working paper “Getting the Biggest Bang for the Buck in Fiscal Policy”:

The lack of legal authority for central banks to issue national lines of credit is not set in stone. Indeed, for the sake of speed in reacting to threatened recessions, it could be quite valuable to have legislation setting out many of the details of national lines of credit but then authorizing the central bank to choose the timing and (up to some limit) the magnitude of issuance. Even when the Fed funds rate or its equivalent is far from its zero lower bound at the beginning of a recession, the effects of monetary policy take place with a significant lag (partly because of the time it takes to adjust investment plans), while there is reason to think that consumption could be stimulated quickly through the issuance of national lines of credit. Reflecting the fact that national lines of credit lie between traditional monetary and traditional fiscal policy, the rest of the government would still have a role both in establishing the magnitude of this authority and perhaps in mandating the issuance of additional lines of credit over the central bank’s objection (with the overruled central bank free to use contractionary monetary policy for a countervailing effect on aggregate demand).

Though not as good as monetary stimulus, National Lines of Credit are also much better than traditional fiscal policy in yielding a high ratio of stimulus to the amount ultimately added to the national debt.

National Rainy Day Accounts. There is a related mode of stabilization policy that I consider superior to National Lines of Credit. The National Rainy Day Accounts described in this passage of my working paper “Getting the Biggest Bang for the Buck in Fiscal Policy” would not add to the national debt at all: 

It is also worth pointing out that, in principle, national lines of credit in times of low demand could be superseded in the long run (at least in part) by a modest level of forced saving in times of high demand,  with the funds from these “national rainy day accounts” released to households in time of recession (and also perhaps in the case of one of a well-defined list of documentable personal financial emergencies).

The National Rainy Day Accounts also have household finance benefits for people who have difficulty saving for emergencies without some external discipline. The main limitations of National Rainy Day Accounts as stabilization policy is (a) that they require advance preparation and (b) the resources of National Rainy Day Accounts might sometimes be exhausted before getting enough stimulus.

Wallace Neutrality Roundup: QE May Work in Practice, But Can It Work in Theory?

Quantitative easing or “QE” is the large scale purchases by a central bank of long-term or risky assets. QE has been used in a big way by the Fed since the financial crisis and by the Bank of Japan since the recent Japanese election, and is an important item on the monetary policy menu of all central banks that have already lowered short-term safe rates to close to zero. Moreover, purchases by the European Central Bank of risky sovereign debt at heavily discounted market prices can rightly be seen as a form of QE–indeed, as a relatively powerful form of QE.  

For monetary stimulus, I favor replacing QE by negative interest rates, made possible by a fee when private banks deposit paper currency with the central bank and establishing electronic money as the unit of account. (See “How and Why to Eliminate the Zero Lower Bound: A Reader’s Guide.”) But my proposal to eliminate the liquidity trap is viewed as radical enough that its near-term prospects are quite uncertain. So understanding quantitative easing (“QE”) remains of great importance for practical discussions of monetary policy. The key theoretical issue for thinking about QE is the logic of Wallace Neutrality. I wrote a lot about Wallace Neutrality in my first few months of blogging, (as you can see by going back to the beginning in 2012 in my blog archive) but haven’t written as frequently about Wallace Neutrality since I turned my attention to eliminating the zero lower bound. This post gives a roundup of some of the online discussion about Wallace Neutrality in the last year or so. 

I should note that I typically don’t even realize that someone has written a response to one of my posts unless someone sends a tweet with “@mileskimball” in it, tells me in a comment, or sends me an email. So I appreciate Richard Serlin letting me know about several posts he and others have written about Wallace Neutrality.  

Richard Serlin 1: Richard has two posts. In the first, published September 9, 2012, “Want to Understand the Intuition for Wallace Neutrality (QE Can’t Work), and Why it’s Wrong in the Real World?” Richard sets the stage this way:

This refers to Neil Wallace’s 1981 AER article, “A Modigliani-Miller theorem for open-market operations”. The article has been very influential today, as it has been used as a reason why quantitative easing can’t work. Here are some example quotes:

“No, in a liquidity trap, if the Fed purchases gold, it does not change the price of gold, just as it will not change the prices of Treasury bonds if it purchases them.” – Stephen Williamson
“The Fed can buy all the government debt it wants right now, and that will be irrelevant, for inflation or anything else.” – Stephen Williamson
“If it were up to me, I would have given Wallace the [Nobel] prize a long time ago, and I think Sargent would say the same. However, not everyone in the profession is aware of Wallace’s contributions, and people who are aware don’t necessarily get as excited about them as I do.” – Stephen Williamson
“…the influence of Wallace neutrality thinking on the Fed is clear from the emphasis the Fed has put on telling the world what it is going to do with interest rates in the future…I have a series of other posts also discussing Wallace neutrality. In fact, essentially all of my posts listed under Monetary Policy in the June 2012 Table of Contents are about Wallace neutrality.” – Miles Kimball

In Wallace’s model, when the Fed prints money and buys up an asset with it, this affects no asset’s price, and doesn’t even change inflation! Amazing claims, but they’re mathematically proven to be true – in Wallace’s model, and with the accompanying assumptions. So the big question is, even in a model, how can claims like this make sense? What could be the intuition for that? 

Brad DeLong: Richard points to this from Brad DeLong as some of the best intuition for Wallace Neutrality that he had found up to that point:

Long ago, Bernanke (2000) argued that monetary policy retains enormous power to boost production, demand, and employment even at the zero nominal lower bound to interest rates:

The general argument that the monetary authorities can increase aggregate demand and prices, even if the nominal interest rate is zero, is as follows: Money, unlike other forms of government debt, pays zero interest and has infinite maturity. The monetary authorities can issue as much money as they like. Hence, if the price level were truly independent of money issuance, then the monetary authorities could use the money they create to acquire indefinite quantities of goods and assets. This is manifestly impossible in equilibrium. Therefore money issuance must ultimately raise the price level, even if nominal interest rates are bounded at zero. This is an elementary argument, but, as we will see, it is quite corrosive of claims of monetary impotence…

His argument, however, seems subject to a powerful critique: The central bank expandeth the money stock, the central bank taketh away the money stock, blessed be the name of the central bank. In order for monetary policy to be effective at the zero nominal lower bound, expectations must be that the increases in the money stock via quantitative easing undertaken will not be unwound in the future after the economy exits from its liquidity trap. If expectations are that they will be unwound, then there is potentially money to be made by taking the other side of the transaction: sell bonds to the central bank now when their prices are high, hold onto the cash until the economy exits from the liquidity trap, and then buy the bonds back from the central bank in the future when it is trying to unwind its quantitative easing policies. A Modigliani Miller-like result applies.

Richard Serlin 1 Again: Richard then gives this rundown of Neil Wallace’s paper itself:

The government prints dollars and buys the single consumption good, which I like to call c’s….

People are going to want to store a certain amount of c’s anyway, because that’s utility maximizing to help smooth consumption. What the government essentially does in this model is say, hey, store your c’s with us instead of at the private storage facility. Give us a c, and we’ll give you some dollars, which are like a receipt, or bond. We’ll then store the c’s – we won’t consume them, we won’t use them for anything (these are crucial assumptions of Wallace, required to get his stunning results) – We will just hold them in storage (implied in the equations, not stated explicitly).

Next period, you give us back those dollars, and we give you back your c’s, plus some return (from the dollar per c price changing over that period). In equilibrium, the return from storing c’s via the dollar route must be equal to the return from storing c’s via the private storage facility route. Or at least the return must be worth the same amount at the equilibrium state prices; so either way you go you can arrange at the same cost in today c’s, the same exact next period payoff in any state that can occur….

It is analogous to Miller-Modigliani, in that if a corporation increases its debt holding, then shareholders will just decrease their personal debt holding by an equivalent amount, so that their total debt stays exactly where it was, which was the amount they had previously calculated to be utility maximizing for them (And there’s a lot of very unrealistic and material assumptions that go with this that have been long acknowledged as such in academic and practitioner finance; when you learn Miller-Modigliani, at the bachelors, masters, and PhD levels – which I have –  they always start by teaching the model and its strong assumptions, and then go into the various reasons why it far from holds in reality. This is long accepted in academic finance; pick up any text that covers MM.)

Richard offers one other intuition for Wallace Neutrality, based on asset pricing principles when asset prices are at their fundamental values:

Suppose dollars are printed and used to buy 10 year T-bonds. Or gold, like in the Stephen Williamson quote at the beginning of this post. And everybody knows (making a Wallace-like assumption) that in five years the T-bonds or gold will be sold back for dollars. We’re making all of the perfect assumptions here: For all investors, perfect information, perfect foresight, perfect analysis, perfect rationality, perfect liquidity,…

Now, what is the price of gold? How is it calculated in this world of perfects?

Well, as a financial asset it’s worth only what it’s future cash flows are. Suppose you are going to hold onto the gold and sell it in one year. Then, what it’s worth is its price in one year (which you know at least in every state – perfect foresight) discounted back to the present at the appropriate discount rate.

But suppose this: During that year that you will be holding the gold in your vault, you are told the government will borrow your gold for five minutes, take it out of your vault, and replace it with green slips of paper with dead presidents, then five minutes later they will take back the green slips and replace back your gold in the vault. Do you really care? This doesn’t affect how much you will get for the gold when you sell it in a year, and as a financial asset that’s all you care about when you decide how much gold is worth today.

If you’re going to hold the gold for ten years, and sell it then, then you only care about what the price of gold will be in ten years. And the price of gold in ten years only depends on what the supply and demand for gold is in ten years. If the government takes 100 million ounces of gold out of private vaults, and put it in its vaults, then puts it back in the private vaults three years later, this has no effect on the supply of gold in ten years. So in ten years the price of gold is the same. And if gold will be the same price in ten years, then it will be worth the same price today for someone who’s not going to sell for ten years anyway.

Jérémie Cohen-Setton and Éric Monnet: A year later, September 6, 2012, Richard wrote a follow-up post: The Intuition for Wallace Neutrality, Part II: Why it doesn’t Work in the Real World. Richard flags an excellent synthesis by Jérémie Cohen-Setton and Éric Monnet on 10th September 2012: Blogs review: Wallace Neutrality and Balance Sheet Monetary Policy. Jérémie and Éric start by explaining why understanding the issues surrounding Wallace Neutrality matters in the real world, with particular reference to Mike Woodford’s conclusions assuming Wallace Neutrality, and then give this summary discussions of Wallace Neutrality by Richard, Brad DeLong, Michael Woodford and me:

Miles Kimball defines Wallace neutrality as follows:  a property of monetary economic models in which differences in the government’s overall balance sheet at moments in time when the nominal interest rate is zero have no general equilibrium effect on interest rates, prices, or non-financial economic activity. Richard Serlin (HT Mark Thoma) writes that in Wallace’s model, when the Fed prints money and buys up an asset with it, this affects no asset’s price, and doesn’t even change inflation!

Brad DeLong and Miles Kimball think that Wallace neutrality has baseline modeling status, in the same manner as Ricardian neutrality. Saying a model has baseline modeling status is saying that it should be the starting point for thinking about how the world works – as it reflects how the simplest economics models behave within the category of “optimizing models.”. The discussion is then about what might plausibly make things behave differently in the real world from that theoretical starting point.  Miles Kimball argues that the difference in the theoretical status of Wallace neutrality as compared to Ricardian neutrality is that we are earlier in the process of putting together good models of why the real world departs from Wallace neutrality. Studying theoretical reasons why the world might not obey Ricardian neutrality was frontier research 25 years ago.  Showing theoretical reasons why the world might not obey Wallace neutrality is frontier research now….

As far as intuition for Wallace Neutrality goes, here is Jérémie and Éric channeling Mike Woodford:

Michael Woodford notes that it is important to note that such “portfolio-balance effects” do not exist in a modern, general-equilibrium theory of asset prices. Within this framework the market price of any asset should be determined by the present value of the random returns to which it is a claim, where the present value is calculated using an asset pricing kernel (stochastic discount factor) derived from the representative household’s marginal utility of income in different future states of the world. Insofar as a mere re-shuffling of assets between the central bank and the private sector should not change the real quantity of resources available for consumption in each state of the world, the representative household’s marginal utility of income in different states of the world should not change. Hence the pricing kernel should not change, and the market price of one unit of a given asset should not change, either, assuming that the risky returns to which the asset represents a claim have not changed.

On reasons why Wallace Neutrality might not hold in the real world, I am pleased to see that Jérémie and Éric reference the Wikipedia article on Wallace Neutrality that Fudong Zhang got started:

The Wikipedia page for Wallace Neutrality – the result of a proposed public service provided by the readers of the Miles Kimball’s blog, Confessions of a Supply-Side Liberal – point to other recent works which invalidate Wallace neutrality based on different relaxed assumptions and novel mechanisms. For example, in Andrew Nowobilski’s (2012) paper, open market operations powerfully influence economic outcomes due to the introduction of a financial sector engaging in liquidity transformation.

Richard Serlin 2: Now for the core of what Richard says in his second post, The Intuition for Wallace Neutrality, Part II: Why it doesn’t Work in the Real World. Richard has kindly given me permission to quote at some length from his nice explanation of the logic behind Wallace Neutrality and why it might not hold in the real world: 

I had gone down various roads in thinking about why the neutrality that worked in Wallace’s model would not work in the real world, and I just wasn’t able to really nail down any of them the way I wanted to, at least not the ones I wanted to. But thinking about this again, the idea came to me. The intuition is this:

Suppose the Fed does buy up 100 million ounces of gold in a quantitative easing. And the people who are savvy, well informed, expert, and rational know that in some years the economy will turn around, and the Fed will just sell back all of those 100 million ounces. So, in 10 years, the supply of gold will be the same as it would have been if the quantitative easing had never occurred. The ownership papers will shift from private parties to the federal government in the interim, but will be back again to private parties like they never left in 10 years. So, no fundamental change to the asset’s value in 10 years.

And if no fundamental change to the asset’s value in 10 years, then no fundamental change to the asset’s value today, as the value today, for a financial asset with no dividends, coupons, etc., is just the discounted present value of the asset’s value 10 years from now.

Now, as should be obvious – especially with gold – not all investors are savvy, well informed, expert, and rational – let alone sane! So, when the price of gold starts to go up, some of them will not sell at that higher price, even though fundamentally the price should not go higher; nothing has changed about the long run, or 10 year, price of gold.

In the Wallace model, and commonly in financial economics models, no problem, arbitrage opportunity! Suppose there are investors who are less than perfectly expert, knowledgeable, and rational – or way less – and they don’t sell when the government buys up the price a little. Who cares. It just takes one expert knowledgeable investor to recognize that there’s an arbitrage opportunity when the price of gold goes up merely because the government is buying it in a QE, and he’ll milk it ceaselessly until the price is all the way back down again and the arbitrage disappears….

Now, for this to work as advertised, first you need 100% complete markets, so you must have a primitive asset (or be able to synthetically construct one) for every possible state at every possible time in the world.

[using Chandler Bing voice] Have you seeeen our world? The number of states just one minute from now is basically infinite. Even the number of significant finitized states over the next day, let alone a path of years, is so large, it’s for all intents and purposes infinite. Thus, try to construct a synthetic asset that pays off the same as gold, now and over time, and you’re not going to come very close. And if you try buying it to sell gold, or vice versa, to get an “arbitrage”, you’re going to expose yourself to a lot of risk.

And this is a key. I think a lot of misunderstanding comes from loose use of the word “arbitrage”. The textbook definition of arbitrage is a set of transactions that has zero risk, zero. It’s 100% risk free. It’s not low risk, as often things that are called arbitrage are. It’s not 99% risk-free. It’s riskless, zero. That’s what makes it so powerful in models, at least one of the things.

Another one of the things that makes it so powerful in models is that it requires none of your own money. If there’s an expert and informed enough investor anywhere, even just a single one, who sees it, it doesn’t matter if he doesn’t have two nickels to rub together, he can do it. He can borrow the money to buy the assets necessary, and at the market interest rate. Or, he can just sign the necessary contracts, for whatever amounts, no matter how big. His credit and credibility are always considered good enough….

Well, what are the problems with that? The usual one you hear is that savvy investors are only a small minority of all investors, and this is especially true of highly expert investors who are highly informed about a given individual asset, or even asset class. And they only have so much money. Eventually, if the government keeps buying in a QE it could exhaust their funds, their ability to counter, by, for example, selling gold they own, or selling gold they don’t own short.

Even rich people and institutions only have so much money and liquidity, or credit. You can’t outlast the Fed, if the Fed is truly determined. Your pockets may be very deep, but the Fed’s pockets are infinite.

So, you usually hear that.

But there’s another reason why the savvy marginal investor is limited in his ability and willingness to push prices back to their fundamentals that I never hear. It’s a powerful and important reason: The more a savvy investor jumps on a mispriced individual asset, the more his portfolio gets undiversified, and that can quickly become dangerous and not worth it.

Miles: Despite having turned my primary attention in relation to monetary policy to eliminating the zero lower bound, I have written a fair amount about QE in the last year. My column “Why the US Needs Its Own Sovereign Wealth Fund” discusses my intuition that Wallace Neutrality will be further from the truth for assets that have the largest risk and term premiums and what this suggests for monetary policy, given that the Fed doesn’t have non-emergency authority to buy corporate stocks and bonds:

…what if longer-term Treasuries and mortgage-backed securities are the wrong assets for the Fed to buy? Most of those rates are already below 3%, so it’s not that easy to push the rates down further. What is worse, when long-term assets already have low interest rates, pushing down those interest rates pushes the prices of those assets up dramatically. So the Fed ends up paying a lot for those assets, and when it later has to turn around and sell them—as it ultimately will need to, to raise interest rates and avoid inflation, it will lose money. Avoiding buying high and selling low is tough when the Fed has to move interest rates to do the job it needs to do. At least economic recovery reduces mortgage defaults and so helps raise the prices of mortgage-backed securities through that channel. But the effects of interest rates on long-term assets cut against the Fed’s bottom line in a way that is never an issue when the Fed buys and sells 3-month Treasury bills in garden-variety monetary policy.

From a technical point of view, once 3-month Treasury bill rates (and overnight federal funds rates) are near zero, the ideal types of assets for “quantitative easing” to work with are assets that (a) have interest rates far above zero and (b) are buoyed up in price when the economy does well. That means the ideal assets for quantitative easing are stock index funds or junk bond funds!

Yet, is the Federal Reserve even the right institution to be making investment decisions like this?…

Why not create a separate government agency to run a US sovereign wealth fund? Then the Fed can stick to what it does best—keeping the economy on track—while the sovereign wealth fund takes the political heat, gives the Fed running room, and concentrates on making a profit that can reduce our national debt….

As an adjunct to monetary policy, the details of what a US Sovereign Wealth Fund buys don’t matter. As long as the fund focuses on assets with high rates of return, the effect on the economy will be stimulative, and the Fed can use its normal tools to keep the economy from getting too much stimulus.

In May 2013, I wrote a full column on quantitative easing: “QE or not QE: Even Economists Need Lessons in Quantitative Easing, Bernanke Style,” sparked by a Martin Feldstein column. There, in relation to Wallace Neutrality, I write:

Once the Fed has hit the “zero lower bound,” it has to get more creative. What quantitative easing does is to compress—that is, squish down—the degree to which long-term and risky interest rates are higher than safe, short-term interest rates. The degree to which one interest rate is above another is called a “spread.” So what quantitative easing does is to squish down spreads. Since all interest rates matter for economic activity, if safe short-term interest rates stay at about zero, while long-term and risky interest rates get pushed down closer to zero, it will stimulate the economy. When firms and households borrow, the markets treat their debt as risky. And firms and households often want to borrow long term. So reducing risky and long-term interest rates makes it less expensive to borrow to buy equipment, hire coders to write software, build a factory, or build a house.

Some of the confusion around quantitative easing comes from the fact that in the kind of economic models that come most naturally to economists, in which everyone in sight is making perfect, deeply-insightful decisions given their situation, and financial traders can easily borrow as much as they want to, quantitative easing would have no effect. In those “frictionless” models, financial traders would just do the opposite of whatever the Fed does with quantitative easing, and cancel out all the effects. But it is important to understand that in these frictionless models where quantitative easing gets cancelled out, it has no important effects. Because in the frictionless models quantitative easing gets canceled out, it doesn’t stimulate the economy. But because in the frictionless models quantitative easing gets cancelled out it has no important effects. In the world where quantitative easing does nothing, it also has no side effects and no dangers. Any possible dangers of quantitative easing only occur in a world where quantitative easing actually works to stimulate the economy!

Now it should not surprise anyone that the world we live in does have frictions. People in financial markets do not always make perfect, deeply-insightful decisions: they often do nothing when they should have done something, and something when they should have done nothing. And financial traders cannot always borrow as much as they want, for as long as they want, to execute their bets against the Fed, as Berkeley professor and prominent economics blogger Brad DeLong explains entertainingly and effectively in “Moby Ben, or, the Washington Super-Whale: Hedge Fundies, the Federal Reserve, and Bernanke-Hatred.” But there is an important message in the way quantitative easing gets canceled out in frictionless economic models. Even in the real world, large doses of quantitative easing are needed to get the job done, since real-world financial traders do manage to counteract some of the effects of quantitative easing as they go about their normal business of trying to make good returns. And “large doses” means Fed purchases of long-term government bonds and mortgage-backed bonds that run into trillions and trillions of dollars. (As I discuss in “Why the US Needs Its Own Sovereign Wealth Fund,” quantitative easing would be more powerful if it involved buying corporate stocks and bonds instead of only long-term government bonds and mortgage-backed bonds.) It would have been a good idea for the Fed to do two or three times as much quantitative easing as it did early on in the recession, though there are currently enough signs of economic revival that it is unclear how much bigger the appropriate dosage is now….

Sometimes friction is a negative thing—something that engineers fight with grease and ball bearings. But if you are walking on ice across a frozen river, the little bit of friction still there between your boots and the ice allow you to get to the other side. It takes a lot of doing, but quantitative easing uses what friction there is in financial markets to help get us past our economic troubles.

In response to one commenter (by email) who thought that QE had not done much either for the stock market or the economy as a whole, I wrote:

But this seems like an argument for a bigger dosage of QE. And it is not clear that the counterfactual is share prices staying the same. Without any QE, the economy would probably have been hurting enough that stock prices would have gone down….

The key point I am trying to make is that it is the ratio of stimulus to undesirable side-effect that matters, not the ratio of stimulus to dollar size of asset purchase. I think you are saying that the Fed has done a lot of QE with relatively little effect, but to the extent that the QE has relatively little effect in undesirable directions as well as relatively little effect in terms of stimulus, the answer is simply to scale up the size of the asset purchases. For example, if a given level of QE has little effect on the level of stock prices and therefore little stimulus, it presumably has relatively little effect on financial stability as well, to the extent financial stability worries have to do with the level of the stock market.  
The one undesirable effect I know of that depends on the size of the asset purchase *as opposed to the size of the stimulus generated,* is the capital losses the Fed will face when it sells the long-term bonds. That is something I write about in my column advocating a US Sovereign Wealth Fund as a way to do a fixed quantum of QE that focuses on assets that would gain more in value from general equilibrium effects than long-term government bonds would: “Why the US Needs Its Own Sovereign Wealth Fund.”

The point

…it is the ratio of stimulus to undesirable side-effect that matters, not the ratio of stimulus to dollar size of asset purchase.

is of course the point I was making in my first post on Wallace Neutrality (and second post on QE) back in June 2012,

“Trillions and Trillions: Getting Used to Balance Sheet Monetary Policy." (There is a similar point in my working paper "Getting the Biggest Bang for the Buck in Fiscal Policy” about National Lines of Credit.“You can read the blog post here, which has a link to the paper.)  

GiveWell: Top Charities →

In my post “Inequality Aversion Utility Functions: Would $1000 Mean More to a Poorer Family than $4000 to One Twice as Rich?” I use math and survey data on inequality aversion to argue that the big gains from redistribution are from taking care of the desperately poor. GiveWell is a website that rates charities in a way consistent with that criterion. Take a look. 

I learned about GiveWell from Michael Huemer’s excellent book The Problem of Political Authority.

Don't Believe Anyone Who Claims to Understand the Economics of Obamacare

Here is a link to my 33d column on Quartz “Don’t believe anyone who claims to understand the economics of Obamacare.”

Here is my original introduction, which was drastically trimmed down for the version on Quartz: 

Republican hatred of Obamacare, and Democratic support for Obamacare, have shut down the “non-essential” activities of the Federal Government. So, three-and-a-half years since President Obama signed the “Patient Protection and Affordable Care Act” into law, and a year or so since a presidential election in which Obamacare was a major issue, it is a good time to think about Obamacare again.

In my first blog post about health care, back in June 2012, I wrote:

I am slow to post about health care because I don’t know the answers. But then I don’t think anyone knows the answers. There are many excellent ideas for trying to improve health care, but we just don’t know how different changes will work in practice at the level of entire health care systems.  

That remains true, but thanks to the intervening year, I have high hopes that with some effort, we can be, as the saying goes, “confused on a higher level and about more important things.”

One thing that has come home to me in the past year is just how far the US health care sector—with or without Obamacare—is from being the kind of classical free market Adam Smith was describing when he talked about the beneficent “invisible hand” of the free market. 

Reactions: Gerald Seib and David Wessel Included this column in their “What We’re Reading” Feature in the Wall Street Journal. Here is their excellent summary:

The key to the long-run impact of Obamacare will be whether it smothers innovation in health care – both in the way it is organized and in the development of new treatments. And no one today can know whether that’ll happen, says economist Miles Kimball. [Quartz]

(In response, Noah Smith had this to say about me and the Wall Street Journal.) This column was also featured in Walter Russell Mead’s post “How Will We Know If Obamacare Succeeds or Fails.” (Thanks to Robert Graboyes for pointing me to that post.) He writes:

Meanwhile, at Quartz, Miles Kimball has a post entitled “Don’t Believe Anyone Who Claims to Understand the Economics of Obamacare.” The whole post is worth reading, but near the end, he argues that the ACA’s effect on innovation could eventually be the most important thing about it’s long-term legacy…

From our perspective, these are both very good places to start thinking about how to measure Obamacare’s impact. Of course, Tozzi’s metric is easier to quantify than Kimball’s: it will be difficult to judge how the ACA is or isn’t limiting innovation. But that doesn’t mean we shouldn’t try: without innovation, there’s no hope for a sustainable solution to the ongoing crisis of exploding health care costs.

I have also been pleased by some favorable tweets. Here is a sampling: