Quartz #57-->In Defense of Clay Christensen: Even the 'Nicest Man Ever to Lecture' at Harvard Can't Innovate Without Upsetting a Few People
Here is the full text of my 57th Quartz column, “Defending Clay Christensen: Even the ‘nicest man ever to lecture’ at Harvard can’t innovate without upsetting a few people,“ now brought home to supplysideliberal.com. It was first published on December 23, 2014. Links to all my other columns can be found here.
I wrote a version of this first as a blog post. I am delighted that my new editor at Quartz, Paul Smalera, liked it enough to publish it in Quartz. (My previous editor, Mitra Kalita, is now overseeing key aspects of Quartz’s global expansion.)
By the way, since I am blogging through Clay’s books (as I have been blogging through John Stuart Mill’s On Liberty) I have a virtual sub-blog on Clay Christensen:
http://blog.supplysideliberal.com/tagged/clay
In the column, I give my take on Clay’s theory as well as defending him personally.
If you want to mirror the content of this post on another site, that is possible for a limited time if you read the legal notice at this link and include both a link to the original Quartz column and the following copyright notice:
© December 23, 2014: Miles Kimball, as first published on Quartz. Used by permission according to a temporary nonexclusive license expiring June 30, 2017. All rights reserved.
**************************************************************************
Clay Christensen is not only the most famous management guru in the world, he is one of the few public figures—other than full time humanitarians or religious leaders—whom people go out of their way to describe as a good person. For example, in the Financial Times in November 2013, Andrew Hill described Clay Christensen, who had just won an award for most influential management thinker for the second time in a row, as “perhaps the nicest man ever to lecture at Harvard Business School.”
So I was surprised to see key Apple executive-turned-tech-entrepreneur Jean-Louis Gassée criticize not only Clay’s theories but also Clay’s character in his Nov. 25, 2014 Quartz article Clayton Christensen should really disrupt his own innovation theories. I want to defend Clay and his theories.
To be clear about where I am coming from, let me say that I can personally vouch for both Clay’s brilliance as a business thinker and his positive personal qualities. On the personal side, I carpooled across the country from Utah to Boston with Clay back in 1977 when I was beginning my freshman year at Harvard College and Clay was beginning to work toward his MBA from Harvard Business School. I have had relatively little contact with Clay since then, but still remember that trip as a bright moment in my life, and consider Clay a friend to this day. My daughter Diana’s experience as a Harvard MBA student in Clay’s class only reinforced my impression that Clay is one of the best human beings I have met.
My views on Clay as a thinker come from reading six of Clay’s books this year:
- The Innovator’s Dilemma: When New Technologies Cause Great Firms to Fail
- The Innovator’s Solution: Creating and Sustaining Successful Growth
- The Innovator’s DNA: Mastering the Five Skills of Disruptive Innovators
- Disrupting Class: How Disruptive Innovation Will Change the Way the World Learns
- The Innovative University: Changing the DNA of Higher Education from the Inside Out
- The Innovator’s Prescription: A Disruptive Solution for Health Care
As an economist, I found them fascinating. One of the hottest areas of economics in the last twenty years has been the border between economics and psychology. One basic idea at that intersection is that people have limitations in their ability to process information and make decisions. This idea that cognition is finite is a key issue in macroeconomics, as Noah Smith and I wrote about in “The Shakeup at the Minneapolis Fed and the Battle for the Soul of Macroeconomics—Again.” But the idea of finite cognition also matters a lot for businesses. Some decisions are hard even for people who spend their careers making those kinds of decisions, and the support of teams of experts.
Clay, in the management theory he has developed with various coauthors, identifies one key factor in how hard a decision is for a generally well-run business: whether it involves taking care of what are already the business’s core customers, or trying to sell to either peripheral customers or people who have never bought from the business before. No business is successful for any significant length of time if it doesn’t do a reasonably good job of taking care of its core customers. But being good at understanding and serving its core customers may make it bad as an organization at understanding and serving peripheral or potential customers.
Clay’s famous warnings about “disruptive innovation” boil down to saying that any set of peripheral or potential customers a business doesn’t serve well—even if those non-core customers look relatively unprofitable—might provide a ladder for a competitor to climb up and eventually overtake that business. And since the main part of a business is designed to serve its core customers, it may need to set up a separate unit to act like a start-up and focus on other potential customers.
When Clay turns to public policy issues in education and health care, the idea of innovative upstarts overtaking an established business by starting with underserved customers or non-customers morphs into the idea of reforming education and health care by finding chinks in the armor of the status quo. The key public policy recommendation I draw from Clay’s logic is that policy should be supportive of organizations doing things in new ways that help people on the margins who find the current systems difficult to navigate, even if those new approaches don’t improve quality for those who are currently well served by the status quo.
Here is Gassée’s own summary of Clay’s theory:
The incumbency of your established company is forever threatened by lower-cost versions of the products and services you provide. To avoid impending doom, you must enrich your offering and engorge your price tag. As you abandon the low end, the interloper gains business, muscles up, and chases you farther up the price ladder. Some day—and it’s simply a matter of time—the disruptor will displace you.
The first charge Gassée makes against Clay is that Clay is a very persuasive, high-priced consultant who advises rival companies:
… in the mid-to-late 1980s, parlayed his position into a consulting money pump. He advised—terrorized, actually—big company CEOs with vivid descriptions of their impending failure, and then offered them salvation if they followed his advice. His fee was about $200,000 per year, per company; he saw no ethical problem in consulting for competing organizations.
In Clay’s case, I get the sense that he is giving almost every company a variant of the same advice, which is more concerned with potential competitors who might not even be in the picture yet, rather than existing competitors. So I can see why two rival companies might both feel comfortable hiring Clay. As to the price, I also find Clay’s insights valuable, so I am willing to go with the default view of economists that if someone is willing to pay a lot of money for something, it is an indication that they find it quite valuable.
Gassée’s next charge is that Clay is arrogant:
The guru and I got into a heated argument while walking around the pool at one of Apple’s regular off-sites. When I disagreed with one of his wild fantasies, his retort never varied: I’m never wrong.
Had I been back in France, I would have told him, in unambiguous and colorful words, what I really thought, but I had acclimated myself to the polite, passive-aggressive California culture and used therapy-speak to “share my feelings of discomfort and puzzlement” at his Never Wrong posture. “I’ve always been proved right…sometimes it simply takes longer than expected,” was his comeback.
Hyperbole—”exaggerated statements or claims not meant to be taken literally”—has its place in conversation (for example, there is every indication that the historical Jesus frequently used hyperbole). So the exact tone of voice and context matter a lot. The management consulting context is one in which hyperbole might be appropriate in order to help counteract an attachment by someone one is advising to the status quo. In that context, saying “I’m never wrong” might mean simply “You should really, really, listen to my advice.” Given the magnitude of Clay’s claims, if Clay sincerely believes in the advice he is giving, as I suspect he does, the sentiment “You should really, really, listen to my advice” is understandable.
Gassée’s last charge is that Clay became defensive and lashed out when his work was challenged by Jill Lepore. Here is what Gassée has to say about that:
Christensen is admired for his towering intellect and also for his courage facing health challenges—one of my children has witnessed both and can vouch for the scholar’s inspiring presence. Unfortunately, his reaction to Lepore’s criticism was less admirable. In a Businessweek interview Christensen sounds miffed and entitled:
“I hope you can understand why I am mad that a woman of her stature could perform such a criminal act of dishonesty”
In this case, fortunately, the context is known. You can see Drake Bennett’s Businessweek interview “Clayton Christensen Responds to New Yorker Takedown of ‘Disruptive Innovation‘” here. Clay told Drake
… she starts instead to try to discredit Clay Christensen, in a really mean way. And mean is fine, but in order to discredit me, Jill had to break all of the rules of scholarship that she accused me of breaking—in just egregious ways, truly egregious ways. In fact, every one—every one—of those points that she attempted to make [about The Innovator’s Dilemma] has been addressed in a subsequent book or article. Every one! And if she was truly a scholar as she pretends, she would have read [those]. I hope you can understand why I am mad that a woman of her stature could perform such a criminal act of dishonesty …
So Clay’s intemperate phrase “criminal act of dishonesty” is about Jill Lepore writing as if Clay hadn’t ever given any answer to the kinds of questions she raises. A specific case later in the interview clarifies what is angering Clay. Here is Drake Bennett’s question:
Another point Lepore makes is that you leave out relevant factors that would challenge your thesis. In the case of the steel industry, you don’t talk about unionization, which was a major difference between U.S. Steel and upstart minimills.
Clay replied:
Yes and no. The world is actually very complicated and big huge books are written about unionization and the impact that it has, and so … other people have addressed that.
If she’s interested, there’s a case that I use in my course about U.S. Steel that occurred in 1989. There the union contract in Mon Valley Works [one of U.S. Steel’s plants] was a huge factor. So, again, if she were thorough on this issue and she Googled it and put in my name and U.S. Steel, that would have come up. But because her purpose was to discredit me rather than look for the truth, she didn’t even look. Are you feeling a little bit about how she’s caused me to feel?
That is, Clay thinks Jill Lepore did not do even the most basic homework to see if Clay had any subtlety to his views. Here, actually, Lepore’s point is about how differential unionization might weaken the evidence for Clay’s theory of disruptive innovation, which Clay’s Harvard Business School case might not have done anything to address, so Lepore’s fundamental point might stand, but she should have made that argument. And while it may be unreasonable to expect someone writing a magazine article to know one’s whole body of work before vigorously criticizing a piece of it, it is reasonable to expect her to try to talk to Clay to get his side before publishing a traditional-style long-read article attacking Clay’s work. This is a point Clay himself makes:
… if she’s interested and wants to help me—she’s just an extraordinary writer—and if she’s interested in the theory or its impact, I mean, come over! I would love to have you openly invite her to come do this, if she’s interested.
(Like Clay, Jill Lepore is at Harvard.)
I think Drake Bennett is right that Clay was quite angry at Jill Lepore’s article:
Consistently described by those who know him as a generous and thoughtful and upbeat person, he is also capable of fury. “Keep asking me questions,” [Clay] said, “it’s helping me.”
But, I am not going to change my view of Clay as one of the best human beings I have met for controlled anger in a situation like that.
No one is perfect. But in order for us to have a hope of becoming better human beings, we need to at least know which direction is up. Despite his flaws, I don’t know anyone who wouldn’t do well to become a little more like Clay in at least some respect.
Matthew Yglesias on the Need to Eliminate the Zero Lower Bound to Avoid Secular Stagnation →
A tweet from Ellie Kesselman pointed me to this piece by Matthew Yglesias. The key passage is
As I’ve been saying for a while, humanity could rid itself of the pesky zero bound problem by eliminating physical currency and creating a situation where nominal interest rates can go negative. Demographic shifts and population aging may someday (like “next few decades” not “later this summer”) soon force us to choose between this option and the world economy falling into a basically permanent recession.
That is, Matthew Yglesias is very worried that the natural interest rate might be below zero on a long term interest rate, and an inability to have negative interest rates would therefore be disastrous. I am less convinced that the natural interest rate will be negative on a long run basis (because I am optimistic about future technological progress), but it is definitely worth being prepared.
You can see links to what I have written on negative interest rates in my bibliographic post “How and Why to Eliminate the Zero Lower Bound: A Reader’s Guide,” and my discussion of issues surrounding the natural interest rate and secular stagnation in “The Medium-Run Natural Interest Rate and the Short-Run Natural Interest Rate” and “On the Great Recession.”
Q&A: Is There Anything to Supply-Side Economics?
Question: Hi Dr. Kimball - So i’m a Larry Kudlow fan- been so since 2005. Do I stand alone here? its easier to find a trend of more critics against Kudlow along with Supply Side Economics. I google SSE and the 1st page is flooded with why it doesn’t work. your thoughts much appreciated.
Answer: I used to watch “The McLaughlin Group” all the time, and liked Larry Kudlow a lot there.
On your question about supply-side economics, It depends on what people mean by “supply-side economics.” At current rates, in my view neither incentive effects nor Keynesian multipliers are large enough for cutting taxes to raise revenue. But leaving that very specific tax issue aside, the supply-side is of crucial importance, much more important for long-run welfare than the demand side. That is a point I make at length in “The Deep Magic of Money and the Deeper Magic of the Supply Side.”
Several of my sub-blogs particularly address the supply side in many of their posts:
To me, that what I say in those posts is supply-side economics.
Carlo Ratti and Matthew Claudel: Top-Down vs. Bottom-Up →
The following quotation is from the Project Syndicate article “Life in the Uber City,” by Carlo Ratti and Matthew Claudel:
As every French fifth-grade student knows, the Internet was invented in Paris. It was called Minitel …
Both Minitel and the Internet were predicated on the creation of digital information networks. Their implementation strategies, however, differed enormously. Minitel was a top-down system; a major deployment effort launched by the French postal service and the national telecommunication operator. It functioned well, but its potential growth and innovation was necessarily limited by its rigid architecture and proprietary protocols.
The Internet, by contrast, evolved in a bottom-up way, managing to escape the telecommunication giants’ initial appeals for regulation. Ultimately, it became the chaotic but revolutionary world-changer that we know today (“a gift from God,” as Pope Francis recently put it).
A key requirement for robust long-run economic growth is to make sure that established players can’t block bottom-up solutions when bottom-up solutions are called for–which is often!
Clay Christensen, Jerome Grossman and Jason Hwang: How to Divide and Conquer Our Health Care Problems
As I discussed in my post “Clay Christensen, Jerome Grossman and Jason Hwang on the Three Basic Types of Business Models,” Clay Christensen and his coauthors in all his business strategy books use a model of three basic types of business models:
- solution shops
- value-added processing (VAP)
- facilitated networks.
In The Innovator’s Prescription (location 375), Clay Christensen, Jerome Grossman and Jason Hwang point out how these different types of business models default to different types of payment structures. Adding some headings:
Solution Shops
Payment almost always is made to solution shop businesses in the form of fee for service. We’ve observed that consulting firms such as Bain and Company occasionally agree to be paid in part based upon the results of the diagnosis and recommendations their teams have made. But that rarely sticks, because the outcome depends on many factors beyond the correctness of the diagnosis and recommendations, so guarantees about total costs and ultimate outcomes can rarely be made. …
Value Added Processing
VAP businesses typically charge their customers for the output of their processes, whereas solution shops must bill for the cost of their inputs. Most of them even guarantee the result. They can do this because the ability to deliver the outcome is embedded in repeatable and controllable processes and the equipment used in those processes. Hence, restaurants can print prices on their menus, and universities can sell credit hours at guaranteed prices. Manufacturers of most products publish their prices and guarantee the result for the period of warranty.
Since they operate in the realms of empirical and precision medicine, VAP businesses in the health-care industry can do the same thing. MinuteClinic posts the prices of every procedure it offers. Eye surgery centers advertise their prices; and Geisinger’s heart hospitals can specify in advance not just the price of an angioplasty procedure, but can guarantee the result. In a new and remarkable agreement with several European governments, Johnson & Johnson has guaranteed that its new drug Velcade will effectively treat a specific form of multiple myeloma that can be diagnosed with a particular biomarker—or it will refund to the health ministry the cost of the full course of therapy. J&J can do this because the treatment is undertaken after a definitive diagnosis has been made. …
Facilitated Networks
Facilitated network business models in health care can be structured to make money by keeping people well; whereas solution shop and VAP business models make money when people are sick.
In particular, facilitated networks often work on some kind of subscription or annual fee for payment.
Clay, Jerome and Jason argue that there are two key steps to making health care less expensive:
- separating out the components of health care according to the most appropriate type of business model, and
- developing better ways of doing things within each category, building on that higher level of focus within each part of health care.
Here is how they say it (with my headings):
The need to separate out components of health care according to appropriate business model:
Many who have written about the problems of health care decry the fact that the value of health-care services being offered by hospitals and doctors is not being measured. To them, we would explain that the reason isn’t that these providers don’t want to provide measurable value; they simply can’t, because under the same roof they have conflated fundamentally different business models whose metrics of output, value, and payment are incompatible with one another. …
Using the clear metrics within each category of health care to innovate further:
The reason why this basic segregation of business models must occur from the outset of disruption is that it will enable accurate measurements of value, costs, pricing, and profit for each type of business. A second wave of disruptive business models can then emerge within each of these three types. Powerful online tools can walk physicians through the process of interpreting symptoms and test results to formulate hypotheses, then help them define the additional data they need to converge upon definitive diagnoses. This will enable lower-cost primary care physicians to access the expertise of—and thereby disrupt—specialist practitioners of intuitive medicine. Likewise, ambulatory clinics will disrupt inpatient VAP hospitals. Retail providers like MinuteClinic, which employ nurse practitioners rather than physicians, need to disrupt physicians’ practices.
Avoiding the trap of thinking everything needs to be done in the solution shop business model:
Hospitals and physicians’ practices have long defended themselves under the banner, “For the good of the patient.” Yet, for the good of the patient, do we really need to leave all care in the realm of intuitive medicine? Much technology has moved past this point, and health-care business models need to catch up. Two landmark reports from the Institute of Medicine—Crossing the Quality Chasm and To Err Is Human—shattered the myth that ever-escalating cost was the price Americans must pay to have the high-quality care that only full-service hospitals staffed by the best doctors can provide.
I find Clay, Jerome and Jason’s indictment of our current health care system as mixing together care appropriate to different business models trenchant. I wish this insight made it into more of the commentary about health care reform.
You can see the rest of my posts tagged “Clay Christensen” here.
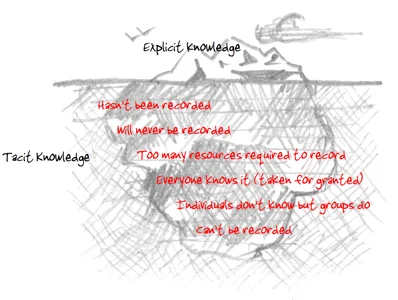
Ricardo Hausman: The Tacit Knowledge Economy
The trouble with this illustration from Shawn Callahan’s post “What do we mean by tacit knowledge” is that it emphasizes only the difficulties of recording knowledge. Economically, the difficulties of getting knowledge into someone’s head are at least as important a difficulty and getting knowledge out of someone’s head.
I highly recommend Ricardo Hausman’s post “The Tacit Knowledge Economy.” Ricardo poses the following revealing puzzle:
Brazil in 2010 was 84.3% urban; its fertility rate was 1.8 births per woman; its labor force had an average of 7.2 years of schooling; and its university graduates accounted for 5.2% of potential workers. These are better social indicators than the United Kingdom had in 1960. …
Brazil is not a unique case: Colombia, Tunisia, Turkey, and Indonesia in 2010 compare favorably to Japan, France, the Netherlands, and Italy, respectively, in 1960. Not only did these countries achieve better social indicators in these dimensions; they also could benefit from the technological innovations of the past half-century: computers, cellphones, the Internet, Teflon, and so on. …
So today’s emerging-market economies should be richer than today’s advanced economies were back then, right?
Wrong – and by a substantial margin. …
Why can’t today’s emerging markets replicate levels of productivity that were achieved in countries with worse social indicators and much older technologies?
Ricardo proposes this answer to the puzzle:
The key to this puzzle is tacit knowledge. To make stuff, you need to know how to make it, and this knowledge is, to a large extent, latent – not available in books, but stored in the brains of those who need to use it.
Getting it there is really tough.
You can see my take on this theme of difficult-to-transfer knowledge in one of my favorite posts, “Two Types of Knowledge: Human Capital and Information.” Here is the key idea there:
Human capital is knowledge that is hard to transfer.
Information is knowledge that is easy to transfer.
Adam Mossoff: The “Common Law Property” Myth in the Libertarian Critique of IP Rights, Part 1 →
I am posting this link to Part 1 of Adam Mossoff’s post on the history of copyright law because I think our copyright law is too restrictive. My interest in copyright policy can also be seen in my post “Copyright,” and from the link post that I am reproducing in full below:
The Wonderful, Now Suppressed, Republican Study Committee Brief on Copyright Law
This is an excellent policy brief that is a well-written, fast, easy read. You can still see it thanks to Maryland Pirates. Alex Tabarrok flagged it here. And Matthew Yglesias has a great discussion of the politics and the economic merits in his post “The Case of the Vanishing Policy Memo.” But on the economic merits, the policy brief speaks well for itself.
Jim O'Neill: A 10-Step Program for India’s Economy →
Having written about India in my column “Will Narendra Modi’s Economic Reforms Put India on the Road to Being a Superpower?”, I was interested to see what Jim O'Neill had to say about how to foster India’s economic growth.
American Wizards
In H. W. Brand’s excellent book American Colossus: The Triumph of Capitalism, 1865-1900he retells this story from Lee Chew, “The Life Story of a Chinaman” (in the collection The Life Stories of Undistinguished Americans, as Told by Themselves, pp. 178-179). The moral of the story is that technology matters, and differences in per capita income matter.
Even more compelling than letters were the actions of emigrants who returned home. Lee Chew grew up on a farm near Canton during the 1860s. Some of the neighbors had left for California, but Lee Chew’s father wished to keep him home and so told him stories of what “foreign devils” the Americans were. They were powerful, with great fire-belching ships and a kind of sorcery that allowed them to light the darkest night and communicate over long distances, but they lacked anything that passed for civilization. Their language was barbaric, they practiced all manner of violence, and they disrespected their ancestors. No correct-thinking Chinese should wish to go to America. Lee Chew had little reason to doubt his father, and he resigned himself to life as a Chinese farmer–until new evidence surfaced.
I was about sixteen years of age when a man of our tribe came back from America and took ground as large as four city blocks and made paradise of it. He put a large stone wall around and led some streams through and built a palace and summer house and about twenty other structures, with beautiful bridges over the streams and walks and roads. Trees and flowers, singing birds, water fowl and curious animals were within the walls. … When his palace and grounds were completed he gave a dinner to all the people, who assembled to be his guests. One hundred pigs roasted whole were served on the tables, with chickens, ducks, geese and such an abundance of dainties that our villagers even now lick their fingers when they think of it. He had the best actors from Hong Kong performing, and every musician for miles around was playing and singing. At night the blaze of lanterns could be seen for miles.
The lesson was lost on no one there, least of all Chew.
The man had gone away from our village a poor boy. Now he returned with unlimited wealth, which he had obtained in the country of the American wizards. … The wealth of this man filled my mind with the idea that I, too, would like to go to the country of the wizards and gain some of their wealth.
Uwe Reinhardt: Does Occupational Licensing Deserve Our Approval? A Review of Work by Morris Kleiner →
I was impressed with Uwe Reinhardt when I met him in person some years ago. And I like what he says in this abstract about occupational licensing. You can get Uwe’s full review at the link above.
Abstract: The licensing of occupations—a very forceful intervention in markets—is pervasive and growing in modern economies. Yet the attention paid to it by economists and economics textbooks has been small. Highly welcome, therefore, has been the extensive and intensive work on this subject by Morris Kleiner. Kleiner’s latest book, titledStages of Occupational Regulation: Analysis of Case Studies(2013), explores the progression of occupational regulation, from mere registration to certification to outright licensing—three distinct stages. Kleiner carefully selects for his analysis a series of occupations representing the stages of regulation, devoting a chapter to each occupation. He uses a variety of statistical approaches to tease out, from numerous databases, what the impact of mild to heavy regulation on labor markets appears to be. Kleiner’s work leads him to call for a pervasive review of occupational regulation in the United States, with a view towards replacing occupational licensure, which introduces the most inefficiency and welfare loss, with mere certification of occupations. That recommendation gains plausibility in an age where cheap computation and data mining makes it possible to protect consumers from low-quality and possibly dangerous services by providing robust, user-friendly information on the quality of services delivered by competing occupations, such as doctors and nurse practitioners.
‘Keep the Riffraff Out!’
Mormonism is a proselyting religion. Close to 35 years ago, I was one of many Mormon missionaries trying to persuade people in Tokyo to become Mormons. And most of you will one time or another see Mormon missionaries at your door, wherever you are in the world.
One of the positive features of a proselyting religion that is not always fully appreciated is that newcomers are fully welcome, as long as they make even a minimal attempt to fit in. And if they so choose, it is not hard for them to become full members of the community.
Sometimes, members of the Mormon Church question the virtue of bringing someone into the community who has enough needs that they are likely to require more help from the community than the amount they are able to help others. But the young women and men serving for a year and a half or two as full-time missionaries and higher Mormon Church authorities quickly overrule such sentiments.
I don’t believe in the supernatural anymore, so I don’t believe in Mormonism. But I do believe in America.
I wish America were a proselyting nation, eager to bring newcomers into the fold. I believe it would be a better world if more of the world’s 7 billion people were Americans. There are many people who would be willing converts to being Americans, but we keep them out.
I have written a lot about immigration policy. For example, see “The Hunger Games is Hardly Our Future: It’s Already Here” and “You Didn’t Build That: America Edition.” But the sentiment “Keep the riffraff out!” shows up in other contexts as well. It is also an important motivating force behind the lobbying for occupational licensing, which I wrote about in “When the Government Says “You May Not Have a Job.” And the sentiment “Keep the riffraff out!” is a serious barrier to affordable housing, as it leads many cities to impose regulations that severely limit the construction of new housing, as Ryan Avent and Matthew Yglesias talk about in their respective books:
The Gated City by Ryan Avent
The Rent Is Too Damn High: What To Do About It, And Why It Matters More Than You Think by Matthew Yglesias.
To me, a central ethical principle is that people are people, and all human beings deserve to be treated as human beings. “Keep the riffraff out!” should not be our first impulse in relation to other human beings.
Quartz #52—>How to Turn Every Child into a 'Math Person'
Here is the full text of my 52d Quartz column, ”How to turn every child into a ‘math person,'” now brought home to supplysideliberal.com. It was first published on August 11, 2014. Links to all my other columns can be found here.
This is now my 5th most popular column, edging out “After Crunching Reinhart and Rogoff’s Data, We Found No Evidence High Debt Slows Growth.” See the whole list of most popular columns and posts here.
If you want to mirror the content of this post on another site, that is possible for a limited time if you read the legal notice at this link and include both a link to the original Quartz column and the following copyright notice:
© August 11, 2014: Miles Kimball, as first published on Quartz. Used by permission according to a temporary nonexclusive license expiring June 30, 2017. All rights reserved.
Last month, the US Math Team took second place in the International Math Olympiad—for high school students—held in Cape Town, South Africa. Since 1989, China has won 20 out of 27 times (including this year), and in the entire history of the Olympiad, the US Math Team has won only 4 out of 55 times, so second place is a good showing. According to the American Mathematical Association website: “team leader Loh noted that the US squad matched China in the individual medal count and missed first place by only eight points.”
Reading about the US Math Team’s performance in the Olympiad this year takes me back to my senior year of high school in 1977 when, having taken 9th place in the US Math Olympiad, I was invited to travel to the International Math Olympiad in Belgrade as an alternate to the 8-member US Math Team. I chose not to go to Belgrade because the Olympiad conflicted with the National Speech Tournament, where my team couldn’t have tied on points for first place without me—while the US Math Team won without needing my help. This profoundly shaped my perception of myself as a “math person.”
Left: an article from 1976 when Miles placed 23rd in the US Math Olympiad; top: in 1977 Miles placed 9th in the competition; bottom: questions from the 1977 USA Math Olympiad.
More than 36 years later, I have come to the view that almost everyone should think of herself or himself as a “math person.” In our column “There’s one key difference between kids who excel at math and those who don’t,” Noah Smith and I wrote this about the often-heard statement: “I’m just not a math person.”
We hear it all the time. But the truth is, you probably are a math person, and by thinking otherwise, you are possibly hamstringing your own career. Worse, you may be helping to perpetuate a pernicious myth—that of inborn genetic math ability.
Not everyone agrees with us. Noah and I got some pushback for our rejection of the idea that inborn math ability is the dominant factor in determining math skill. So I did some more reading in the psychology literature on nature vs. nurture for IQ and for math in particular. The truth is even more interesting than the simple story that Noah and I told.
Math ability is not fixed at birth
Three facts run contrary to the idea that inborn mathematical ability is a dominant factor in determining whether or not someone is good at math compared to others of the same age.
First, it is a reasonable reading of the very inconsistent evidence from twin studies to think that genes account for only about half of the variation in mathematical skill among kids. For example, this 2007 National Institutes of Health Public Access twin study, using relatively transparent methods, estimates that genes account for somewhere in the range from 32% to 45% of mathematical skill at age 10. That leaves 55% to 68% of mathematical skill to be accounted for by other things—including differences in individual effort. (Other estimates of the percentage of variation of mathematical skill in kids due to genes range all the way from 19% to 90%. )
Second, a remarkable fact about IQ tests, including the mathematical components of IQ tests, is that every generation looks a lot smarter than the previous generation. This steady increase in performance on IQ tests is known as “the Flynn effect” after the political philosopherJames Flynn, who discovered this remarkable fact. The American Psychological Association’s official report “Intelligence: Knowns and Unknowns” says:
… performance has been going up ever since testing began. The “Flynn effect” is now very well documented, not only in the United States but in many other technologically advanced countries. The average gain is about 3 IQ points per decade.
At that rate, an IQ test from 100 years ago would put an average American today at an IQ of 130—in the top 2.5% of everyone back then. The American Psychological Association’s report goes on to say:
The consistent IQ gains documented by Flynn seem much too large to result from simple increases in test sophistication. Their cause is presently unknown, but three interpretations deserve our consideration. Perhaps the most plausible of these is based on the striking cultural differences between successive generations. Daily life and occupational experience both seem more “complex” (Kohn & Schooler, 1973) today than in the time of our parents and grandparents. The population is increasingly urbanized; television exposes us to more information and more perspectives on more topics than ever before; children stay in school longer; and almost everyone seems to be encountering new forms of experience. These changes in the complexity of life may have produced corresponding changes in complexity of mind.
In other words, although people a century ago were good at many things, many of them would have struggled with the kinds of abstract problems IQ tests focus on.
(As a simple example of how math standards have risen, my father tells me that when he was in high school, people thought calculus was too advanced for high school students. Nowadays, about one of every six high school students takes calculus in the US.)
Third (and I wish the research were clearer about this for math specifically), the fraction of differences in IQ that seem genetically linked increases dramatically with age. For children, about 45% of differences in IQ appear to be genetic, while for adults, about 75% of differences in IQ appear to be genetic. Think about that. How could it be that genes matter more and more as people get older—even though the older you get, the more environmental things have happened to you? What I think is the most plausible answer, is that the genes are influencing what people do and what they do in turn affects their IQ.
The “love it and learn it” hypothesis
No one yet knows exactly how genes, environment, and effort interact to determine mathematical skill. In light of the evidence above, let me propose what I call the “love it and learn it” hypothesis. This hypothesis has three elements:
For anyone, the more time spent thinking about and working on math, the higher the level of mathematical skill achieved.
Those who love math spend more time thinking about and working on math.
There is a genetic component to how much someone loves math.
Despite emphasizing time spent on math as the driver of math skill, this can explain why identical twins look more alike on math skills than fraternal twins. Since time spent dealing with math matters, it allows plenty of room for the average person to be better at math now than a hundred years ago. And the effect of loving math on math experience and therefore math skill is likely to only grow with time.
To get better at math, act like someone who loves math
If the “love it and learn it” hypothesis is true, it gives a simple recommendation for someone who wants to get better at math: spend more time thinking about and working on math. Best of all: spend time doing math in the kinds of ways people who love math spend time doing math. Think of math like reading. Not everyone loves reading. But all kids are encouraged to spend time reading, not just for school assignments, but on their own. Just so, not everyone loves math, but everyone should be encouraged to spend time doing math on their own, not just for school assignments. If a kid has a bad experience with trying to learn to read in school, or is bored with the particular books the teacher assigned, few parents would say “Well, maybe you just aren’t a reader.” Instead, they would try hard to find some other way to help their kid with reading and to find books that would be exciting for their particular kid. Similarly, if a kid has a bad experience trying to learn math in school, or is bored with some bits of math, the answer isn’t to say “Well maybe you just aren’t a math person.” Instead, it is to find some other way to help that kid with math and to find other bits of math that would be exciting for their particular kid to help build her or his interest and confidence.
The way a teacher presents a mathematical principle or method in class may not work for you—or, as Elizabeth Green suggested in the New York Times, the whole American pattern of K-12 math instruction may be fatally flawed. If you loved math, you would think about that principle or method from many different angles and look up and search out different mathematical resources, until you found the angle that made most sense to you. Even if you don’t love math, that would be a good way to approach things.
Many people think that because they can’t understand what their math teacher is telling them, it means they can’t understand math. What about the possibility that your teacher doesn’t understand math? Some people are inspired to a life-long love of math by a great math teacher; others are inspired to a life-long hatred of math by an awful math teacher. If you are unlucky enough to have an awful math teacher, don’t blame math for your teacher’s failings.
Cathy O’Neil—who blogs at mathbabe.org—describes well what I like to call “slow-cooked math”:
There’s always someone faster than you. And it feels bad, especially when you feel slow, and especially when that person cares about being fast, because all of a sudden, in your confusion about all sort of things, speed seems important. But it’s not a race. Mathematics is patient and doesn’t mind.
Being good at math is really about how much you want to spend your time doing math. And I guess it’s true that if you’re slower you have to want to spend more time doing math, but if you love doing math then that’s totally fine.
I was lucky to have a dad and older brother who showed me a bit of math early on, in a way that was unconnected to school. Then in school, I spent at least as much time on math when I wasn’t supposed to be doing math as when I was. It was a lot more fun doing math when I wasn’t supposed to be doing math than when I was.
For one thing, when I did it on my own, I could do it my own way. But also, there were no time limits. It didn’t matter if it took me a long time. And nothing seemed like a failure.
I spent a lot of time doing math. And very little of that math was done under the gun of a deadline. I spent some time on literal tangents in geometry and trigonometry. But I spent a lot more time on figurative tangents, running into mathematical dead ends. When Euclid told King Ptolemy “there is no Royal Road to geometry,” it had at least two meanings:
Everyone—even a king or queen—has to work hard if he or she wants to learn geometry or any other bit of higher math.
The path to learning geometry, or math in general, is not always a straight line. You may have to circle around a problem for a long time before you finally figure out the answer.
What can be done
I feel acutely my own lack of expertise in math education for students younger than the college students I teach. Fortunately, there are a wealth of practical suggestions for teaching and learning math by others who know more than I do, or have a different perspective from their own experience.
Noah and I received many comments in response to our post but the comments I learned the most from were from these people, who let me turn their comments into guest posts on my blog:
Matt Waite: How I Faced My Fears and Learned to Be Good at Math
Marjorie Drysdale: Even When You Can Do Math, You May Not Love It
Jing Liu: Show Kids that Solving Math Problems is Like Being a Detective
Matt Rognlie on Misdiagnosis of Difficulties and the Fear of Looking Foolish as Barriers to Learning
In Green’s article “Why Americans Stink at Math,” she talks about how differently math is taught in Japanese classrooms, and how we should hope that we might someday get that kind of math instruction in the US. The key difference is that in Japan, the students are led by very carefully designed lessons to figure out the key math principles themselves. That kind of teaching can’t easily be done without the right kind of teacher training—teacher training that is not easy to come by in the United States.
But some teachers at least encourage their students to follow a “slow-cooked math” approach where they can dig in and wrap their heads around what is going on in the math, without feeling judged for not understanding instantly. Elizabeth Cleland gives a good description here of how she does it.
Even when a student is lucky enough to have good teachers at school, a little extra math on the side can help a lot. Kids who arrive at school knowing even a tiny bit of math will have more confidence in their math ability and will probably start out liking math more. Even quite young kids will be interested in a Mobius strip made out of paper where a special twist makes what looks like two sides into just one side. And putting blocks of different lengths next to each other as in a Montessori addition strip board is exactly how I have always pictured addition in my head.
A Montessori addition strip board. Image via jsmontessori.com
Extra math doesn’t all have to come from parents. In some towns, enough Little League soccer coaches are found for almost every kid to be on a soccer team. And even I was once drafted as a Cub Scout Den Leader. If people realized the need, many more adult leaders for math clubs for elementary and middle school kids could be found. In addition to showing kids some things themselves, math club leaders can do a lot of good just by checking out and sorting through the growing number of great math videos and articles online, as well as old-style paper-and-ink books.
I use Wikipedia regularly as a math reference. (There is no reason to think Wikipedia is any less reliable than the typical math textbook; textbooks are not 100% error-free either.) I have a post on logarithms and percent changes that is one of the most popular posts on my blog. (Maybe it is the evocation of piano keyboards and slide rules, or the before and after pictures of Ronald Reagan.) And Susan Athey, the first woman to win the John Bates Clark Medal for best American economist under forty, highly recommends Glenn Ellison’s Hard Math for Elementary School as a resource for math clubs. All of that just scratches the surface of the resources that are out there.
The obvious issue raised by the “love it and learn it” hypothesis is that some people may not start out loving math, and some may never love math. Acting as if you love math when you don’t may work, but it can be painful. So it is important to figure out what can be done to instill a love of math. Even if they only know a little math themselves, people who can get kids who don’t start out loving math to come to love it are a national treasure. As the brilliant business guru Clay Christensen (among others) has pointed out, in an age when lectures from the best lecturers in the world can be posted online, the kind of help students need on the spot is the help of a coach.
For too long, we have depended too heavily on overburdened math teachers who have remarkably little time in school to actually teach math, and whom the system has deprived of the kind of training they need to teach math as well as it can be taught. It is time for all of us to take the responsibility for learning math and doing what we can to help others learn math–just as we all take responsibility for learning to read and doing what we can to help others learn to read.
Most of us who participated as kids in a sport or other competitive pursuit remember a coach who got us to put in a lot more effort than we ever thought we would. Math holds out the hope of victory not just in a human competition, but in understanding both the visible universe and the invisible Platonic universe. There is no impossibility theorem saying there can’t be math coaches in every neighborhood who make the average kid want to gain that victory.
That is the end of the column proper, but I have also collected here as a postscript a few memories, ideas and suggestions that had to be cut out of the Quartz column to make the column flow well. I added some headings to make it clear where each bit fits in.
I spent at least as much time on math when I wasn’t supposed to be doing math as when I was: The teacher might have been talking about social studies, but I was finding the prime factorizations of all the numbers from 1 to 400 by writing “2 ×” for every other number “3 ×” for every third number, “5 ×” for every fifth number, etc.—and then repeating that process for every other even number, every third multiple of 3, every fifth multiple of 5, and so on). The prime factorizations I learned from that satisfyingly tedious task I distracted myself with in elementary school came in handy when I took my SAT’s. And to this day, the way I get a hotel room number firmly into my memory is by doing its prime factorization.
Nothing seemed like a failure: At one point I knew just enough algebra to know that doing the same thing to both side of an equation left it a true equation. So for a long time, I transformed equations endlessly with no idea at all of where I was trying to go with those equations. Later on, when I actually had a purpose in mind for what I wanted to accomplish with a bit of algebra, I was able to draw on all of that experience just wandering around in algebra-land. And because I knew what it was like to do math without having any particular objective, I was able to appreciate how important it was keep the objective clearly in mind when there was an objective.
Proofs on other topics to get kids ready for proofs in Geometry class: Many kids who do well with arithmetic and algebra have trouble with geometry class in middle school or high school. It is often very hard to understand the idea of a proof when can’t see any reason to doubt the proposition to be proved in the first place. It is much better to get kids used to the idea of a proof earlier on in a context where the proof tells them something that doesn’t seem obvious. My favorite is the proof that there are an infinite number of primes. (There is a whole page of Youtube videos to choose from on this.) And a lot of kids wonder if imaginary numbers are numbers at all. The proof that complex numbers with an imaginary components obey all the rules of arithmetic and algebra and therefore can be treated as legitimate numbers not only answers a question kids really have, but uses concepts from “The New Math” that confused many kids in the 1960’s in a way that is obviously useful.
Math resources I found useful:
The “Hungarian Problem Books” of challenging math problems
Resources to check out that might be good but that I don’t have any experience with:
Khan Academy videos are at least free! Here is a set of videos about the Khan academy, including a TED talk by Salman Kahn and a “60 Minutes” segment and a talk by Bill Gates about the Khan Academy.
Hands-on Equations for algebra
PhotoMath: “Point your smartphone’s camera towards a mathematical expression and PhotoMath instantly displays a correct result, also showing the step by step process it used to arrive at the answer.”Suggested by Niels Andeweg
Note: if you want to advertise your tool or method for math instruction here, I encourage you to advertise it in a comment that you post in the comment box below. When I moderate the comments, I will approve comments that advertise tools or methods for math instruction like that unless I have reason to believe there is something wrong with that tool or method.
John Cochrane: Larry Summers' Martin Feldstein Speech →
I love this post by John Cochrane.
Quartz #50—>Odious Wealth: The Outrage is Not So Much Over Inequality but All the Dubious Ways the Rich Got Richer
Here is the full text of my 50th Quartz column, “Odious Wealth: The Outrage is Not So Much Over Inequality but All the Dubious Ways the Rich Got Richer,” now brought home to supplysideliberal.com. It was first published on June 30, 2014. Links to all my other columns can be found here.
If you want to mirror the content of this post on another site, that is possible for a limited time if you read the legal notice at this link and include both a link to the original Quartz column and the following copyright notice:
© June 30, 2014: Miles Kimball, as first published on Quartz. Used by permission according to a temporary nonexclusive license expiring June 30, 2017. All rights reserved.
Concern about income inequality, and the even more striking inequality in wealth in the United States, is a key theme for the 2014 US congressional elections and has made Thomas Piketty’s book Capital in the Twenty-First Century a surprise bestseller. There are many reasons to be concerned about wealth inequality itself, regardless of the source of that inequality, but it is hard to pursue a discussion on the topic for long before someone makes a claim about whether the wealthy acquired their money in a deserving way. Partisans on the political left and right know which side of this argument they are supposed to emphasize: many who feel the government needs more revenue conveniently argue as if almost all wealth comes from underhanded, unscrupulous skullduggery, while many who feel the government needs less revenue conveniently argue as if almost all wealth were created by the likes of Steve Jobs, who brought us i-everything. But unlike these partisan stories, in every list of 1,500 or so billionaires, many deserve their wealth while others deserve very little of the wealth they have. While in some cases the principles for whether wealth is deserved or not are obvious, in other cases they are quite subtle.
To start with an easy category, wealth obtained by deceit is illegitimate. For example, given the way tobacco companies lied about the dangers of smoking,the gigantic legal judgments against them seem appropriate (though it is too bad how big a share of that money went into the pockets of lawyers). And although the magnitude of the crime might not be as great, GM’s recently outed behavior in hiding problems with ignition switches has a disturbing resonance with the earlier behavior of the tobacco companies. As these examples make clear, standard legal principles often make it possible to take away wealth obtained by deceit once that deceit is well established. But a greater hatred of deceit on the part of juries, judges, and legislators would help in further neutralizing this form of wealth.
If undeserved wealth always arose in cases where the logic was as simple as that for deceit, and were similarly reprehensible from a criminal or civil law point of view, then the issue of undeserved wealth could be appropriately handled in the courts. In an IMF paper, Harvard Economics professor Michael Kremer and Northwestern University Economics professor Seema Jayachandran make the intriguing proposal that debt incurred by a non-democratic government (after the appropriate international organization has declared that the debt is not in the interests of the people of a country) should be considered “odious debt” that later (and hopefully better) governments of that country need not pay back.
We could similarly talk about “odious wealth”—wealth that is hateful in its origin. But our instincts about the merits of different means of acquiring wealth often go astray. Let me take two extreme examples: old songs that people love and the kind of “vulture capitalism” whose reputation helped sink Mitt Romney’s chances in the 2012 presidential election.
There is currently a dispute over whether songs recorded before 1972 should continue to earn royalties. By naming their bill to extend royalties to pre-1972 recordings the “Respecting Senior Performers as Essential Cultural Treasures Act or “RESPECT” Act, congressmen George Holdings and John Coyners are using the fact that the musicians who recorded songs before 1972 (that we still listen to 42 years later) inspire feelings of gratitude, since songs of lasting popularity give many listeners much more pleasure than those listeners have paid for the right to listen to those songs. But the prospect of that very gratitude, plus 42 years of royalties, would have provided more than enough motivation for musicians to work hard back in 1971 to make great songs, if they had the ability.
Forty-two years is a long time. And money coming in the near future looks (and is) more valuable than money coming in the more distant future. And even songs that last typically get more play in their early years. So at the time a musician is working hard on a song, the prospect of 42 years of royalties and undying fame should, to a surprisingly close approximation, be just as motivating as, say, 80 years of royalties and undying fame. So we don’t need to extend royalties to pre-1972 recordings to bolster the confidence of musicians making songs now that they will be properly rewarded for their efforts. And on the downside, charging royalties for pre-1972 songs has the potential to inhibit the development of internet and satellite radio—and in particular how often people get to listen to the best pre-1972 songs on internet and satellite radio. So there is a lot of downside, not much upside to extending royalties to pre-1972 recordings. But the folks who would earn those royalties, if they are still alive, are attractive recipients of the money, even in cases where they are relatively wealthy.
By contrast, few ways of getting wealth seem less attractive than acquiring companies and then making them more profitable by laying off many of the employees. In August 29, 2012, Matt Taibbi wrote in the Rolling Stone essay “Greed and debt: the true story of Mitt Romney and Bain Capital:”
A man makes a $250 million fortune loading up companies with debt and then extracting million-dollar fees from those same companies, in exchange for the generous service of telling them who needs to be fired in order to finance the debt payments he saddled them with in the first place. …
Instead of building new companies from the ground up, we took out massive bank loans and used them to acquire existing firms, liquidating every asset in sight and leaving the target companies holding the note.
This is what I am calling “vulture capitalism.” But vultures have an important place in the ecosystem. Just like literal vultures, who help clear away dead carcasses, vulture capitalists help in the difficult process of moving workers from making and doing things that people don’t need as much anymore to making and doing things that people are eager to pay for. For example, Mitt Romney helped unwind K-B Toys, whose toys could no longer compete with video games. This was enormously painful for the employees of K-B Toys, who were ultimately sent on their way in an arduous transition to new jobs (and some to early retirement). But an enormous amount of good work has been accomplished by former employees of K-B Toys in new jobs with efforts that would have been squandered on trying to make unwanted toys if K-B Toys had been kept limping along for a few more years.
Since they are unlikely to get much gratitude from their brutal but useful work, vulture capitalists have to be rewarded with money. Otherwise, who would want to do that task of dismantling companies and letting go of people and other resources that should be devoted to other purposes?
None of this is to say that the incentives for vulture capitalism are precisely right. It is unfortunate when, as is too often the case, the efforts of highly trained professionals are focused on transactions that make sense only because of quirks of the tax law. But the basic idea that the old must sometimes be dismantled to provide the human and non-human building blocks for new things is sound. And if something that painful is going to happen, it sometimes makes sense to say as Jesus said to Judas: “What you are about to do, do quickly.” The wealth earned by vulture capitalists may then look like the 30 pieces of silver Judas was given for betraying Jesus, but it must be considered legitimate, nonetheless, because the job needs to be done.
There are two points to take away. First, it is not right to treat all large fortunes as odious wealth (or as otherwise illegitimate in origin) or to treat all large fortunes as beneficent wealth. Second, without careful analysis, our instincts will often lead us astray about which is which.
Although people complain a lot about wealth and income inequality, I suspect that a great deal of that anger comes from how the rich made their fortunes. An ideal version of capitalism—the version in the economic models taught in introductory economics classes around the world—would make it impossible to get rich without doing great good for society. There are certainly areas where doing great good for society is not understood and therefore not appreciated. But there are also many areas where the wrong things are rewarded because of market distortions, or where the government piles on rewards beyond those that are needed.
Among market distortions, lies and deception are a key category. But it is also a problem that the legal remedies available to deal with lies and deception are not matched by any ability to bring a legal tort claim for, say, raising the planet’s temperature by burning coal.
Among excessive rewards caused by the government, bailouts without increases in equity requirements big enough to prevent future bailouts are especially unfair. But actions by the government to protect the profits and business models of firms already in place by standing in the way of firms doing new things in new ways can in the long run be just as damaging. And in the digital age, copyright law is long overdue for reevaluation.
Wealth and income inequality are a topic of perennial fascination. But the heat has been turned up not only by increases in such inequality, but also by the feeling that the 2008 financial crisis and the Great Recession suggest that something is fundamentally wrong with our economic system. Among the many reasons to redesign the monetary plumbing of our economic system to avoid a repeat of the Great Recession, one of the most important is to help us gain clarity on the many long-run issues we face, of which economic inequality is one of the most difficult to deal with.