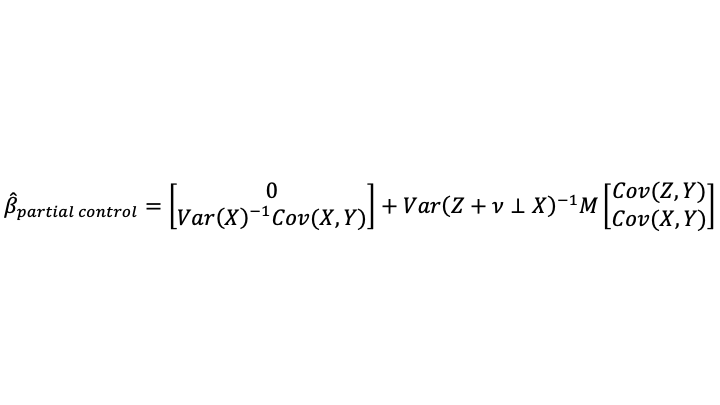In “Eating Highly Processed Food is Correlated with Death” I observe:

In observational studies in epidemiology and the social sciences, variables that authors say have been “controlled for” are typically only partially controlled for. The reason is that almost all variables in epidemiological and social science data are measured with substantial error.

In the comments, someDude asks:

"If the coefficient of interest is knocked down substantially by partial controlling for a variable Z, it would be knocked down a lot more by fully controlling for a variable Z. "

Does this assume that the error is randomly distributed? If the error is biased (i.e. by a third underlying factor), I would think it could be the case that a "fully controlled Z" could either increase or decrease the the change in the coefficient of interest.

This post is meant to give a clear mathematical answer to that question. The answer, which I will back up in the rest of the post, is this:

Compare the coefficient estimates in a large-sample, ordinary-least-squares, multiple regression with (a) an accurately measured statistical control variable, (b) instead only that statistical control variable measured with error and (c) without the statistical control variable at all. Then all coefficient estimates with the statistical control variable measured with error (b) will be a weighted average of (a) the coefficient estimates with that statistical control variable measured accurately and (c) that statistical control variable excluded. The weight showing how far inclusion of the error-ridden statistical control variable moves the results toward what they would be with an accurate measure of that variable is equal to the fraction of signal in (signal + noise), where “signal” is the variance of the accurately measured control variable that is not explained by variables that were already in the regression, and “noise” is the variance of the measurement error.

To show this mathematically, define:

Y: dependent variable

X: vector of right-hand-side variables other than the control variable being added to the regression

Z: scalar control variable, accurately measured

v: scalar noise added to the control variable to get the observed proxy for the control variable. Assumed uncorrelated with X, Y and Z.

Then, as the sample size gets large:

Define the following notation for the part of the variance of Z and of the variance of Z+v that are orthogonal from X (that is, the parts that are unpredictable by X and so represents additional signal from Z that was not already contained in X, plus the variance of noise in the case of Z+v). One can call this “the unique variance of Z”:

I put a reminder of the partitioned matrix inversion formula at the top of this post. Using that formula, and the fact that the unique variance of Z is a scalar, one finds:

Defining

the OLS estimates are given by:

When only a noisy proxy for the statistical control variable is available (which is the situation 95% of the time), the formula becomes:

I claimed at the beginning of this post that the coefficients when using the noisy proxy for the statistical control variable were a weighted average of what one would get using only X on the right-hand side and what one would get using accurately measured data on Z. Note that what one would get using only X on the right-hand side of the equation is exactly what one would get in the limit as the variance of the noise added to Z (which is Var(v)) goes to infinity. So adding a very noisy proxy for Z is almost like leaving Z out of the equation entirely.

The weight can be interpreted from this equation:

As noted at the beginning of the post, the right notion of the signal variance is the unique variance of the accurately measured statistical control variable. The noise variance is exactly what one would expect: the variance of v.

I have established what I claimed at the beginning of the post.

Some readers may feel that the limitation of Z being a single scalar variable is a big limitation. It is worth noting that the results apply when adding many statistical control variables or their proxies, one at a time, sequentially. Beyond that, noncommutativity makes the problem more difficult: the commutativity of a scalar with the other matrices was important for the particular strategy used in the simplifications above.

Conclusion: Almost always, one has only a noisy proxy for a statistical control variable. Unless you use a measurement error model with this proxy you will not be controlling for the underlying statistical control variable. You will only be partially controlling for it. Even if you do not have enough information to fully identify the measurement error model you must think about that measurement error model and report a range of possible estimates based on different assumptions about the variance of the noise.

Remember that any departure from the absolutely correct theoretical construct can count as noise. For example, one might think one has a totally accurate measure of income, but income is really acting as a proxy for a broader range of household resources. In that case, income is a noisy proxy for the household resources that were the correct theoretical construct.

I strongly encourage everyone reading this to vigorously criticize any researcher who claims to be statistically controlling for something simply by putting a noisy proxy for that thing in a regression. This is wrong. Anyone doing it should be called out, so that we can get better statistical practice and get scientific activities to better serve our quest for the truth about how the world works.

Here are links to other posts that touch on statistical issues:

• Let's Set Half a Percent as the Standard for Statistical Significance

• Statistically Controlling for Confounding Constructs is Harder than You Think—Jacob Westfall and Tal Yarkoni

• Examining the Statistics in “Math at Home Adds Up to Achievement in School” by Talia Berkowitz, Marjorie Schaeffer, Erin Maloney, Lori Peterson, Courtney Gregor, Susan Levine and Sian Beilock

• Who Leaves Mormonism?

• Less Than 6 or More than 9 Hours of Sleep Signals a Higher Risk of Heart Attacks

• Hints for Healthy Eating from the Nurses’ Health Study

• Carola Binder—Why You Should Get More Vitamin D: The Recommended Daily Allowance for Vitamin D Was Underestimated Due to Statistical Illiteracy

• Eating Highly Processed Food is Correlated with Death

• The Carbohydrate-Insulin Model Wars

• Data on Asian Genes that Discourage Alcohol Consumption Explode the Myth that a Little Alcohol is Good for your Health

• New Evidence on the Genetics of Homosexuality

• Eggs May Be a Type of Food You Should Eat Sparingly, But Don't Blame Cholesterol Yet

• Cousin Causality

• Henry George Eloquently Makes the Case that Correlation Is Not Causation