A Partisan Nonpartisan Blog: Cutting Through Confusion Since 2012
An excellent choice. I have been very impressed with Michael Barr during the time we overlapped at the University of Michigan. Michael did a lot to craft Dodd-Frank, which while imperfect is much better than alternatives being discussed now, and needs to be defended.
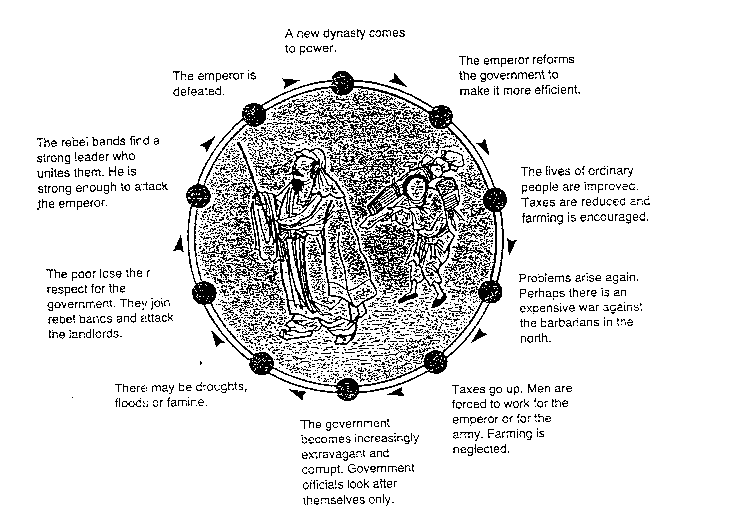
Section 21 of John Locke's 2d Treatise on Government: “On Civil Government” has remarkable resonances with the Chinese idea of the "Mandate of Heaven." This idea maintained that while the imperial Chinese government maintained the Mandate of Heaven by wise rule it was the legitimate judge over its subjects. But when the imperial Chinese government misbehaved, it lost the Mandate of Heaven; attempting to obtain justice then required war. the previous Section 20, which I discussed in "If the Justice System Does Not Try to Deliver Justice, We Are in a State of War," talks about a government misbehaving. Section 21 then contrasts society under a reasonably just government and a state of war in which one hopes for justice from military victory:
To avoid this state of war (wherein there is no appeal but to heaven, and wherein every the least difference is apt to end, where there is no authority to decide between the contenders) is one great reason of men’s putting themselves into society, and quitting the state of nature: for where there is an authority, a power on earth, from which relief can be had by appeal, there the continuance of the state of war is excluded, and the controversy is decided by that power. Had there been any such court, any superior jurisdiction on earth, to determine the right between Jephtha and the Ammonites, they had never come to a state of war: but we see he was forced to appeal to heaven. “The Lord the Judge (says he) be judge this day between the children of Israel and the children of Ammon,” Judg. xi. 27. and then prosecuting, and relying on his appeal, he leads out his army to battle: and therefore in such controversies, where the question is put, who shall be judge? It cannot be meant, who shall decide the controversy; every one knows what Jephtha here tells us, that the Lord the judge shall judge. Where there is no judge on earth, the appeal lies to God in heaven. That question then cannot mean, who shall judge, whether another hath put himself in a state of war with me, and whether I may, as Jephtha did, appeal to heaven in it? of that I myself can only be judge in my own conscience, as I will answer it, at the great day, to the supreme judge of all men.
Does Good Win in the End?
But let's take a look at the idea that military victory is positively correlated with justice. If a benevolent God does not yet exist, then this requires an argument.
Martin Luther King said, memorably,
The arc of the moral universe is long, but it bends toward justice.
Quote Investigator identifies antecedents of this saying. Unitarian minister and Transcendentalist Theodore Parker published an 1853 volume of sermons with this passage:
Look at the facts of the world. You see a continual and progressive triumph of the right. I do not pretend to understand the moral universe, the arc is a long one, my eye reaches but little ways. I cannot calculate the curve and complete the figure by the experience of sight; I can divine it by conscience. But from what I see I am sure it bends towards justice.
Things refuse to be mismanaged long. Jefferson trembled when he thought of slavery and remembered that God is just. Ere long all America will tremble.
and Morals and Dogma of the Ancient and Accepted Scottish Rite of Freemasonry, copyright 1871 had this passage:
We cannot understand the moral Universe. The arc is a long one, and our eyes reach but a little way; we cannot calculate the curve and complete the figure by the experience of sight; but we can divine it by conscience, and we surely know that it bends toward justice. Justice will not fail, though wickedness appears strong, and has on its side the armies and thrones of power, the riches and the glory of the world, and though poor men crouch down in despair. Justice will not fail and perish out from the world of men, nor will what is really wrong and contrary to God’s real law of justice continually endure.
In the absence of the supernatural there is still one reason that history is tilted toward victory of good over evil. Those who can cooperate with others who are unlike them can form larger coalitions than those who can only cooperate with others similar to them. The strategy of cooperating with others who are similar can be pushed a long way: each of us is built around a collection of genetically near-identical cells, with reproduction monopolized by a few germ-line cells much as beehives are built around collections of genetically closely related individuals with reproduction monopolized by the queen bee and the drones. But assuming that strategy of cooperating with similar individuals is pushed to the limit on both sides of a conflict, the side that can also manage cooperation among unlike individuals or unlike groups of individuals will have a big advantage. While not all the way there, the ability to cooperate with unlike individuals or groups of individuals is one step toward agape, the kind of love the early disciples of Jesus talked about.
But far short of reaching a high form of love, the victory of those with a greater ability to cooperate with unlike individuals can bring progress that merits being described as a victory of good against evil. I have in mind the decline in violence over the course of history that Steven Pinker writes about in The Better Angels of Our Nature—a book I highly recommend.
In any individual battle, evil (however defined) may win, but the dice are loaded in favor of goodness that is associated with an ability to cooperate with those who are different.
Conversely, the dice are loaded against those who cannot cooperate with those who are different from them. Hitler provides a good example. Because Hitler was not willing to cooperate with Jews, Nazi Germany lost access to scientific talent important for the war effort. Because Hitler could not cooperate with Stalin, he had to fight a two-front war. Because Hitler could not cooperate with Slavs whom his troops liberated from Stalin, he could not consolidate his hold on the Ukraine as well. If Hitler had not let ideology get in the way of the war effort he led, he would have been more likely to win. But if he had not been motivated by ideology, things might not have gotten to that point in the first place.
This may not be as much to hang one's hat on in hopes for the victory of good over evil as one might wish, but other than my unfounded native optimism, it is all I have.
Link to the article above
Other commentators get close to the views I expressed in "Alexander Trentin Interviews Miles Kimball about Establishing an International Capital Flow Framework." In the first article above, Greg Ip interviewed Mervyn King, Fred Bergsten and Joseph Gagnon, writing this:
Protectionism can change the patterns of a country’s exports and imports, but not the overall balance.
Rather, deeper economic forces are at work. A trade surplus means a country consumes less than it produces and thus saves a lot. A deficit means the opposite. ... the persistence and magnitude of Chinese and German surpluses and U.S. deficits suggest actual policy decisions are at work.
This comes by interfering with currency markets. As Mr. King notes, a country with a weak economy and a trade deficit would expect its currency to fall to boost exports and restrain imports. That can’t happen if exchange rates can’t move, as is the case with China and Germany, though for different reasons. ...
Messrs. Bergsten and Gagnon suggest a new approach to prevent China from reverting to its old ways: When a country buys dollars to hold down its currency for competitive advantage, the U.S. should respond proportionately by purchasing that country’s currency. They also recommend the U.S. go beyond current law, which requires the U.S. to discourage currency manipulation in new trade pacts, by prohibiting it outright.
Notice that currency manipulation is often a matter of keeping an exchange rate the same when it should appreciate, rather than always being a matter of making one's currency depreciate. So currency manipulation cannot be defined by exchange rates. It needs to be defined by official purchases of foreign assets or other active policy to hold down an exchange rate.
The case of Germany is more complex:
Germany is a tougher challenge. Since adopting the euro in 1999, it hasn’t controlled its own currency. However, it did win competitive advantage over its neighbors in the currency union. Labor-market reforms restrained domestic wages. In 2007, a payroll tax cut, which made German labor more competitive, was financed with an increase in the value-added tax, which exempted exports.
I argued that Germany should in part return to having its own currency in "How the Electronic Deutsche Mark Can Save Europe." Short of that, Germany has a responsibility to manage its trade surpluses within the euro zone in other ways. As between the euro zone and the rest of the world, rules against purchase of non-euro-zone foreign assets without permission from other countries would go a long way.
I emphasize in "Alexander Trentin Interviews Miles Kimball about Establishing an International Capital Flow Framework" that monetary interest rate policy is not a problem and can be done by each currency area with only its own interests in mind since other countries can neutralize the main worrisome effects of other countries' interest rate policy with their own interest rate policy while leaving country that initially changed its interest rate policy with the stimulus or restraining effect it needs once all these interest rate movements have been scaled up appropriately. It is purchases of foreign assets that have big spillover effects for the rest of the world that cannot be neutralized without neutralizing the effect the initial purchaser of foreign assets desired.
In the second article shown above, Justin Fox discusses options for how Germany could spend more to reduce its trade surplus.
The last article above is about David Malpass, Trump's nominee for Treasury’s undersecretary for international affairs. David Malpass wants more stable exchange rates, but in many cases that would make things worse by perpetuating trade imbalances. As I mentioned above, currency manipulation often takes the form of countries' acting to keep their exchange rates the same when their currencies should move in order to better balance trade. Attacking official, unilaterally decided purchases of foreign assets is a more appropriate way to identify and combat currency manipulation.
Besides often perpetuating trade imbalances, a big problem with exchange rates that are too stable is that they make stabilization through monetary policy much more difficult. In effect, a country that maintains a fixed or nearly fixed exchange rate with some other country has used up many of its degrees of freedom stabilization policy to keep that exchange rate fixed.
If every country (or currency zone that is not too big) has full freedom in interest rate policy, while needing permission to purchase foreign assets, then each country can stabilize its own economy without artificial trade surpluses or deficits. There would still be a need to try to address the consequences different saving rates in different countries, but that is the next level up in improving the international trade architecture from the first step of banning official foreign asset purchases without permission.
Journalist Greg Ip makes a better case for economics in public policy than many economists themselves do. Here is an excellent passage from the article shown above, partly based on his interview of my classmate and coauthor Doug Elmendorf (whom I wrote about in my unsuccessful plea "The New Republican Majority Should Keep Doug Elmendorf as Director of the Congressional Budget Office"):
“Informed analysis will sometimes be wrong, but I’d rather bet on informed analysis than ignorant guesses,” says Douglas Elmendorf, who ran the CBO from 2009 to 2015 and oversaw its original estimates of the Affordable Care Act, known as Obamacare.
Economic analysis exposes the trade-offs inherent in all policy choices. Import tariffs protect some workers but hurt consumers; a higher minimum wage helps low-skilled workers who have jobs but makes it harder for others to find jobs; eliminating minimum required benefits for health insurance makes coverage cheaper for some consumers but more expensive for others. Identifying these effects “doesn’t mean everyone will agree. But at least people can make decisions with their eyes open,” says Mr. Elmendorf.
Unbiased analysis doesn’t guarantee good decisions, but it makes really bad ones less likely.
Four weeks ago I posted Part 1. And here are the other posts I have put up to honor my Dad since his death on November 21, 2016 (a little over six months ago):
You will learn a lot about Mormonism from watching this video and Part 1: particularly why someone who has thought deeply about many issues might be committed to Mormonism.
I am sad that my University of Michigan Survey Research Center colleague Eleanor Singer died on June 3.
Link to the Powerpoint file for all the slides in this post. For this post only, I hereby grant blanket permission for reproduction and use of material in this post and the Powerpoint file linked above, provided that proper attribution to Miles Spencer Kimball and a link to this post are included in the reproduction. This is beyond the usual level of permission I give here for other material on this blog to which I hold copyright.
In my post "There Is No Such Thing as Decreasing Returns to Scale" and my Storify stories "Is There Any Excuse for U-Shaped Average Cost Curves?" and "Up for Debate: There Is No Such Thing as Decreasing Returns to Scale," I criticize U-shaped average cost curves as a staple of intermediate microeconomics classes. But what should be taught in place of U-shaped average cost curves? This post is my answer to that question: returns to scale and imperfect competition in market equilibrium.
In order to talk about the degree of returns to scale and the degree of imperfect competition, we need a measure of each. The following notation is helpful:
The Degree of Returns to Scale
The degree of returns to scale can be measured by the percent change in output for a 1% change in inputs. I use the Greek letter gamma for the degree of returns to scale:
when there is only a single input in the amount x. (Note that throughout this post I use the percent change concepts and notation from "The Logarithmic Harmony of Percent Changes and Growth Rates" and write as equalities approximations that are very close when changes are small.)
According to the awkward, but traditional terminology, a degree of returns to scale equal to one is "constant returns to scale." A degree of returns to scale greater than one is "increasing returns to scale." As for a degree of returns to scale less than one, make sure to read "There Is No Such Thing as Decreasing Returns to Scale."
If more than one input is used to produce the firm's output, a convenient way to gauge the increase in inputs is to look at the change in total cost holding factor prices fixed. This gives an aggregate of all the different factors weighted by the initial factor prices. Notice that for the standard production technology notion of returns to scale it doesn't matter if factor prices are actually unchanging as the firm changes its level of output; holding factor prices fixed is simply a way to get an index for total factor quantities akin to the way real GDP is measured. Using the percent change in total cost with factor prices held fixed to gauge the percent change in inputs, the degree of returns to scale with multiple factors is:
Remember that this equation is about what happens when a firm changes the quantity of its output, always producing that output in a minimum cost way given those fixed factor prices. If factor prices or technology are changing, then this equation does not hold.
I argue that the degree of returns to scale will typically be declining in the quantity of output. I base this in part on the idea that a fixed cost coupled with a constant marginal cost is the base case we should start from as economists. Here is why the degree of returns to scale declines with the level of output when a firm has a fixed cost coupled with a constant marginal cost:
According to the derivation above, the degree of returns to scale gamma is equal to AC/MC. Thus, when a firm has a fixed cost coupled with a constant marginal cost for the product whose cost is depicted, the degree of returns to scale declines with the level of the output for that product. What is more, if marginal cost MC is constant, the degree of returns to scale gamma = AC/MC has the same shape as the average cost curve AC, though the vertical scale for the degree of returns to scale would have 1 in place of MC.
The Degree of Imperfect Competition
The degree of imperfect competition can be measured by how far above its marginal revenue a firm will want to set its price: the desired markup ratio p/MR. I use the Greek letter mu for the desired markup ratio. Since a firm tries to set its price so that marginal revenue equals marginal cost, this is also how far above its marginal cost a firm will want to set is price. This actual markup ratio p/MC can be different from the desired markup ratio p/MR over periods of time when the firm doesn't have full price flexibility, but in long-run equilibrium, the actual markup ratio P/MC should be equal to the desired markup ratio p/MR.
The desired markup ratio that measures the degree of imperfect competition is closely related to the price elasticity of demand a firm faces, but goes up when the price elasticity of demand the firm faces goes down. I use the Greek letter epsilon for the price elasticity of demand faced by a firm. The key identity can be derived as follows:
Here is a table giving the desired markup ratio for various values of the price elasticity of demand faced by a firm:
Price Elasticity of Demand Faced by a Firm epsilon Desired Markup Ratio mu
1 infinity
1.5 3
2 2
2.5 1.67
3 1.5
4 1.33
5 1.25
6 1.2
7 1.17
8 1.14
10 1.11
11 1.1
21 1.05
101 1.01
infinity 1
There are several noteworthy aspects about this table. First, if a firm has a marginal cost of zero, in long-run equilibrium it will seek out a price at which the price elasticity of demand it faces is equal to 1. The infinite markup ratio corresponds to a positive price divided by a zero marginal cost. I plan to talk about the market equilibrium for this case in a future post.
If a firm has any positive marginal cost, then in long-run equilibrium, regardless of what other firms do, it will keep raising its price until it reaches a price at which the price elasticity of demand it faces is greater than 1, unless it can get away with providing an infinitesimal quantity at an infinite price. (Being able to get away with providing an infinitesimal quantity at an infinite price is unlikely.) Therefore with a positive marginal cost, the desired markup ratio will be finite and greater than one.
A higher desired markup ratio corresponds a lower price elasticity of demand. And a higher desired markup ratio corresponds to more imperfect competition. The desired markup ratio is a very convenient way to measure the degree of imperfect competition.
Market Equilibrium
The graph at the top of this post illustrates market equilibrium. I return to that graph below. For the logic behind market equilibrium, let me quote from my paper "Next Generation Monetary Policy":
Given free entry and exit of monopolistically competitive firms, in steady state average cost (AC) should equal price (P): if P > AC, there should be entry, while if P < AC there should be exit, leading to P=AC in steady state. Price adjustment makes marginal cost equal to marginal revenue in steady state. Thus, with free entry, in steady state,
where by a useful identity γ is equal to the degree of returns to scale and μ is a bit of notation for the desired markup ratio P/MR. The desired markup ratio is equal in turn to the price elasticity of demand epsilon divided by epsilon minus one:
Remarkably, in long-run equilibrium, after both price adjustment and entry and exit, the degree of returns to scale must be equal to the degree of imperfect competition as measured by the desired markup.
I am going to make four key simplifications to make it easier to understand market equilibrium. First, I will assume that the market equilibrium is symmetric so that each firm sells the same amount q. Second, I will assume, at least for the benchmark case that the elasticity of demand for the entire industry's output is zero. That is, customers are perfectly happy to shift from buying one firm's output to buying another firm's output at the elasticity epsilon if they can get a better deal, but they insist on a certain amount of the category of good provided by the industry. Using the letter Q for the total sales in the industry, that means
Q=nq
n=Q/q
q=Q/n
Third, I will assume that the price elasticity of demand a firm faces—and therefore its desired markup ratio—depends only on the number of firms in the industry. Fourth, I will assume that all fixed costs are flow fixed costs rather than being sunk. It is interesting to relax each of these assumptions, but it would be hard to understand those cases without first learning the simplified case I am presenting here. (The most difficult to relax is the symmetry assumption. Relaxing that assumption is least likely to meet the cost-benefit test in the tradeoff between tractability and realism.)
Let me reprise the graph at the top of this post to explain how it illustrates market equilibrium:
This graph is really two interlocking graphs. On the right, the degree of returns to scale and the degree of imperfect competition as measured by the desired markup ratio are shown in relation to the output of a typical firm. On the left, the degree of returns to scale and the degree of imperfect competition as measured by the desired markup ratio are shown in relation to the number n of firms in the industry.
The degree of returns to scale declines with output as explained above. For given total sales in the industry Q, that means that the degree of returns to scale increases with the number of firms in the industry.
The degree of imperfect competition as measured by the desired markup ratio decreases with the number n of firms in the industry. For given total sales in the industry Q, that means that the degree of imperfect competition as measured by the desired markup ratio increases with a typical firm's output q.
The assumption that—other things equal—the degree of imperfect competition declines with the number of firms is intuitive—and I believe correct in the real world. But I should note that there is a very popular model—the Dixit-Stiglitz model—that is popular in important measure because it makes the degree of imperfect competition as measured by the desired markup ratio constant, regardless of how many or few firms there are. The Salop model gives a degree of imperfect competition as measured by the desired markup ratio that declines with the number of firms. But the Salop model is less convenient technically than the Dixit-Stiglitz model. Innovation could be valuable here. A model that had an attractive story, was technically convenient and had a desired markup ratio declining in the number of firms should be able to attract a subsantial number of users. In any case, I stand by the claim that to model the real world, one should have the desired markup ratio declining in the number of firms in the industry.
The intersection on the right shows the long-run equilibrium output of a typical firm in this industry. The intersection on the left shows the long-run equilibrium number of firms in the industry.
When mu > gamma. Though this could be questioned, think of entry and exit happening at a slower pace than price adjustment. (I discuss the relationship between some other adjustment speeds in "The Neomonetarist Perspective.") Once prices have adjusted, MC = MR. So if the degree of imperfect competition mu = p/MR is greater than the degree of returns to scale gamma = AC/MC it means that p > AC and there will be entry. As n rises, AC and p will come closer together until they are equal at the intersection on the left side of the graph.
When mu < gamma. On the other hand, If the degree of imperfect competition mu = p/MR is less than the degree of returns to scale gamma = AC/MC, it means that p < AC and there will be exit. As n falls, AC and p will come closer together until they are equal at the intersection on the left side of the graph.
To summarize:
If mu > gamma, firms enter.
If gamma > mu, firms exit.
In either case, as n adjusts, the quantity of a typical firm's output also changes.
Comparative Statics
Let's consider four thought experiments. First, consider an increase in total sales Q by the industry. This shifts out both curves that are written in terms of Q:
The prediction is that both the number of firms and the output of a typical firm will increase, while both the degree of returns to scale and the degree of imperfect competition will fall. Because the curve showing the desired markup as a function of the number of firms does not shift, the reduction in the the desired markup only occurs as new firms actually enter. The degree of returns to scale overshoots: it drops most right after the increase in total industry sales Q, then gradually rises again as new firms enter and the quantity produced by each firm declines.
Second, consider reduction in the (flow) fixed cost. This cases the returns to scale (gamma) curves on both sides to shift downward:
The prediction is that the number of firms will increase, while the size of a typical firm decreases, and that both the degree of returns to scale and the degree of imperfect competition will fall. Because the desired markup curves does not shift, the desired markup only falls as new firms actually enter, which is likely to be gradual. As in the first experiment, the degree of returns to scale overshoots in the sense of dropping most at first.
With the marginal cost unchanged, the fall in the desired markup ratio leads to a reduction in price. That would expand the size of the industry if the elasticity of demand for the industry product category as a whole were nonzero. That in turn would require the results of the first experiment in order to analyze.
Third, consider a reduction in marginal cost. This causes the returns to scale curves on both sides to shift up, since returns to scale equals AC/MC, and because it includes average fixed cost, AC does not fall as much as MC. However, the effect of MC on AC means that the gamma = AC/MC curves do not rise vertically by as large a percentage as MC falls.
The prediction is that the output of a typical firm will rise, while the number of firms will decline. The degree of returns to scale and degree of imperfect competition rise in the long run. But note that this is because of improved performance of the industry in reducing costs. The equilibrium desired markup ratio rises less than the degree of returns to scale curve, which in turn rises by a smaller percentage than MC falls. The price will be lowest before firms have had a chance to exit—indeed it will initially fall by the full percentage of the decline in MC—but will remain lower in the new long-run equilibrium than in the old long-run equilibrium.
Again, if the elasticity of demand for industry output as a whole is nonzero, the decline in price would lead Q to increase (more at first, somewhat less later on), so the results of the first experiment would be necessary to fully analyze what would happen.
Fourth, consider an increase in the price elasticity of demand for any given number of firms. This might be described as the market becoming "more price-competitive." Both desired markup curves fall:
The prediction is that in the long run the number of firms falls, while the output of the typical firm rises. This might be called a "shakeout" of the industry. Because the industry has become more price-competitive, the number of firms falls. Someone coming from the ancient "Structure-Conduct-Performance" paradigm for Industrial Organization might be confused because the concentration of the industry goes up, yet the performance of the industry improves: the degree of imperfect competition as measured by the desired markup falls, as does the degree of returns to scale in long-run equilibrium.
With MC unchanged, the desired markup and therefore the price falls most right at first, before firms have had a chance to exit. Then the price comes up somewhat, but remains lower than in the initial long-run equilibrium. If the price elasticity of demand for the entire industry's output is nonzero, then Q will increase, especially at first, which will complicate the analysis in ways that the first experiment can help navigate.
Conclusion
In my view, the foregoing analysis is
more on-target than U-shaped average cost curves in relation to the real world
more interesting than U-shaped average cost curves
no harder than U-shaped average cost curves, if one sticks to the simplifications I made. What I have laid out above is difficult, but U-shaped average cost curves are also difficult.
Therefore, it seems better to me to teach returns to scale and imperfect competition in market equilibrium than it is to teach U-shaped average cost curves. In any case, there are always tradeoffs. When it is impossible to teach both, what I have laid out in this post is the opportunity cost for teaching U-shaped average cost curves. I hope you will agree it represents a high opportunity cost, indeed.
Both of these are ungated. Ken Rogoff's abstract gives a good sense of the review and response:
Jeffrey Hummel provides an extremely thoughtful and detailed review, which is welcome, even if there are a number of places where I don’t quite agree with his interpretations, emphasis, and analysis. For example, the notion that central banks already can use helicopter money to solve the zero bound, and that there is little need for negative interest-rate policy in the next deep financial crisis, is dubious. It is also important to stress that the book is about the whole world and not just the United States; there are good reasons why many other advanced economies may find it attractive to move away from the status quo on cash much more quickly than the United States will. Importantly, deciding how to move to a less-cash society should be looked at as a question of calibration, not an all-or-nothing proposition, and not something that needs to be done quickly.
"Justice" in Chinese Characters: "seigi." Image source.
The mere existence of something called a "justice system" does not entitle it to respect. It earns respect by satisfying three conditions, corresponding to three points in my discussion in "John Locke: When the Police and Courts Can't or Won't Take Care of Things, People Have the Right to Take the Law Into Their Own Hands":
To some extent, imperfection on either condition 2 or 3 can be compensated for by doing well on the other of these two conditions. For example, assuming superiority over having people judge their own cases (not hard), either of
would entitle a "justice system" to respect as a justice system without shudder quotes.
Note that sheer power is a big factor in meeting or exceeding condition 3. Thus, as a matter of realpolitik, the nominally designated "justice system" often deserves respect because of its great superiority in execution judgments, as long as its judgments are reasonably good.
Delivering on judgments has two key components:
In the 1st half of section 20 of his 2d Treatise on Government: “On Civil Government”, John Locke emphasizes the pretrial aspect of delivering justice, presumably because of its greater difficulty:
But when the actual force is over, the state of war ceases between those that are in society, and are equally on both sides subjected to the fair determination of the law; because then there lies open the remedy of appeal for the past injury, and to prevent future harm: but where no such appeal is, as in the state of nature, for want of positive laws, and judges with authority to appeal to, the state of war once begun, continues, with a right to the innocent party to destroy the other whenever he can, until the aggressor offers peace, and desires reconciliation on such terms as may repair any wrongs he has already done, and secure the innocent for the future;
In the 2d half of section 20, John Locke emphasizes the importance of accuracy and unbiasedness:
nay, where an appeal to the law, and constituted judges, lies open, but the remedy is denied by a manifest perverting of justice, and a bare-faced wresting of the laws to protect or indemnify the violence or injuries of some men, or party of men, there it is hard to imagine any thing but a state of war: for where ever violence is used, and injury done, though by hands appointed to administer justice, it is still violence and injury, however coloured with the name, pretences, or forms of law, the end whereof being to protect and redress the innocent, by an unbiassed application of it, to all who are under it; where ever that is not bona fide done, war is made upon the sufferers, who having no appeal on earth to right them, they are left to the only remedy in such cases, an appeal to heaven.
What is obvious is that accurately delivering justice is a good thing. The nuance here is that, just as a company that does shoddy work not only does a bad thing but also may lose customers, a "justice system" that does shoddy work not only does a bad thing but also may lose respect. A "justice system" that loses people's respect is often spoken of as having lost its "legitimacy." Legitimacy in this sense is the natural law that judges the civil law in action.
The August 2013 National Geographic article "Sugar Love (A not so sweet story)" by Rich Cohen collects some powerful quotations from experts describing sugar as a slow poison. It also gives some of the slavery-flavored history of sugar. (If Eric Eustace Williams first Prime Minister of Trinidad and Tobago is right, slavery beginning with the triangle trade was a key source of racism as well. He said "Slavery was not born of racism; rather, racism was the consequence of slavery.")
Here are some key passages from pages 87 and 96 about sugar (the pages in between show beautiful pictures of sugary foods by photographer Robert Clark):
"It seems like every time I study an illness and trace a path to the first cause, I find my way back to sugar."
Richard Johnson, a nephrologist at the University of Colorado Denver, was talking to me in his office in Aurora, Colorado..."Why is it that one-third of adults [worldwide] have high blood pressure, when in 1900 only 5 percent had high blood pressure?" he asked. "Why did 153 million people have diabetes in 1980, and now we're up to 347 million? Why are more and more Americans obese? Sugar, we believe, is one of the culprits, if not the major culprit."
... Haven Emerson at Columbia University pointed out that a remarkable increase in deaths from diabetes between 1900 and 1920 corresponded with an increase in sugar consumption. And in the 1960s the British nutrition expert John Yudkin conducted a series of experiments in animals and people showing that high amounts of sugar in the diet led to high levels of fat and insulin in the blood—risk factors for heart disease and diabetes. But Yudkin's message was drowned out by a chorus of other scientists blaming the rising rates of obesity and heart disease instead on cholesterol caused by too much saturated fat in the diet.
As a result, fat makes up a smaller portion of the American diet than it did 20 years ago. Yet the portion of America that is obese has only grown larger. The primary reason, says Johnson, along with other experts, is sugar, and in particular, fructose. Sucrose, or table sugar, is composed of equal amounts of glucose and fructose, the latter being the kind of sugar you find naturally in fruit. ... (High-fructose corn syrup, or HFCS, is also a mix of fructose and glucose—about 55 percent and 45 percent in soft drinks. The impact on health of sucrose and HFCS appears to be similar.)
... Over time, blood pressure goes up, and tissues become progressively more resistant to insulin. The pancreas responds by pouring out more insulin, trying to keep things in check. Eventually a condition called metabolic syndrome kicks in, characterized by obesity, especially around the waist; high blood pressure; and other metabolic changes that, if not checked, can lead to type 2 diabetes, with a heightened danger of heart attack thrown in for good measure. As much as a third of the American adult population could meet the criteria for metabolic syndrome set by the National Institutes of Health. ...
"It has nothing to do with its calories," says endocrinologist Robert Lustig of the University of California, San Francisco. "Sugar is a poison by itself when consumed at high doses."
Books referred to by the article:
Related Story: How the Calories In/Calories Out Theory Obscures the Endogeneity of Calories In and Out to Subjective Hunger and Energy
