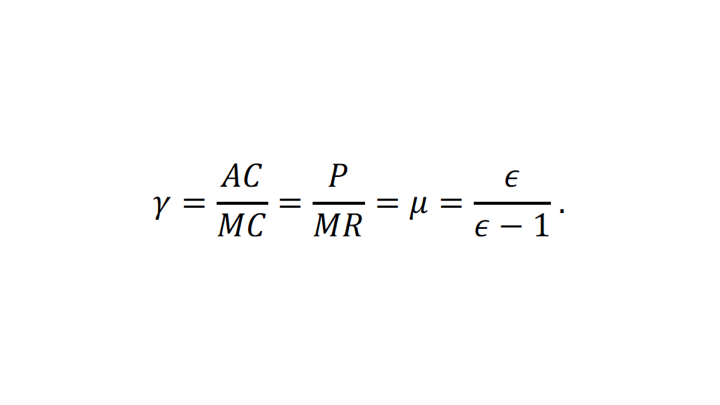On September 7, 2016, I gave a talk at the Mercatus Center conference on “Monetary Rules in a Post-Crisis World.” You can see it here:  Next Generation Monetary Policy: The Video. (And here is a recently revised version of the Powerpoint file.) I have written those ideas out more carefully in a paper I have submitted to the Journal of Macroeconomics (Update: now published in the Journal of Macroeconomics), which co-sponsored the conference. Here is a link to the paper as published that you can download. Below is an earlier version of the text of that working paper as a blog post. 

Abstract: This paper argues there is still a great deal of room for improvement in monetary policy. Sticking to interest rate rules, potential improvements include (1) eliminating any effective lower bound on interest rates, (2) tripling the coefficients in the Taylor rule, (3) reducing the penalty for changing directions, (4) reducing interest rate smoothing, (5) more attention to the output gap relative to the inflation gap, (6) more attention to durables prices, (7) mechanically adjusting for risk premia, (8) strengthening macroprudential measures to reduce the financial stability burden on interest rate policy, (9) providing more of a nominal anchor.

Monetary policy is far inside the production possibility frontier. We can do better. That is what I want to convince you of with this paper.

The worst danger we face in monetary policy during the next five years is complacency. I worry that central banks are patting themselves on the back because the world is finally crawling out of its business cycle hole. It is right to be grateful that things were not even worse in the aftermath of the Financial Crisis of 2008. But dangers abound, including (a) the likelihood that lesson that higher capital requirements are needed to avoid financial crises will be forgotten by key policy-makers, (b) the possibility of a dramatic collapse of Chinese real estate prices, and (c) the not-so-remote chance of a serious trade war.

A longer-term danger is that the rate of improvement in monetary policy will slow down as monetary policy researchers are drawn into simply justifying what central banks already happen to be doing. The assumption that people know what they are doing and are already following the best possible strategy may have an appropriate place in some areas of economics, but is especially inapt when applied to central banks. For one thing, the field of optimal monetary policy is very young, and its influence on central banks even more younger. For another, it is not easy to optimize in the face of complex political pressures and many self-interested actors eager to cloud one’s understanding with false worldviews. 

Advances in monetary policy cannot come from armchair theorizing alone. trying ideas out is the only way to make a fully convincing case that they work—or don’t. But in general, the value of experimentation in public policy is underrated. Because central banks are usually in a good position to reverse something they try that doesn’t work, they are in an especially good position to do policy experiments for which a good argument can be made even if it is not 100 percent certain the experiment will be successful. 

The Value of Interest Rate Rules

Because optimal monetary policy is still a work in progress, legislation that tied monetary policy to a specific rule would be a bad idea. But legislation requiring a central bank to choose some rule and to explain actions that deviate from that rule could be useful. To be precise, being required to choose a rule and explain deviations from it would be very helpful if the central bank did not hesitate to depart from the rule. Under this type of a rule, the emphasis is on the central bank explaining its actions. The point is not to directly constrain policy, but to force the central bank to approach monetary policy scientifically by noticing when it is departing from the rule it set itself and why.

So far, even without legislation, the Taylor Rule—essentially a description of the policy of the Fed under Volcker and Greenspan—has served this kind of useful function. Economists notice when the Fed departs from the Taylor Rule and talk about why.

The Taylor Rule has served another function: as a scaffolding for describing other words. Many important alternatives to the Taylor rule can readily be described as a modification of one of the Taylor Rule’s parameters or as the addition of an additional variable to the Taylor Rule.

In recent years, a shift toward purchasing assets other than short-term Treasury bills has complicated the specification of monetary policy. But Ricardo Reis, in his 2016 Jackson Hole presentation, argues that once the balance sheet is sufficiently large (about $1 trillion), it is again interest rates that matter after that. That is the perspective I take here.

What follows is, in effect, a research agenda for interest rate rules—a research agenda that will take many people to complete. The following sections discuss the following:

1. eliminating the zero lower bound or any effective lower bound on interest rates
2. tripling the coefficients in the Taylor rule
3. reducing the penalty for changing directions
4. reducing the presumption against moving more than 25 basis points at any given meeting
5. a more equal balance between worrying about the output gap and worrying about fluctuations in inflation
6. focusing on a price index that gives a greater weight to durables
7. adjusting for risk premia
8. pushing for strict enough leverage limits for financial firms that interest rate policy is freed up to focus on issues other than financial stability.
9. having a nominal anchor.

Considering these possible developments in monetary policy is indeed only a research program, not a done deal. For each item individually, I have enough confidence research will ultimately vindicate it to be willing to state my views assertively. But though I don’t know which, it is likely that I have made some significant error in my thinking about at least one of the nine.

1.     Eliminating the Zero Lower Bound and Any Effective Lower Bound for Nominal Rates

Eliminating any lower bound on interest rates is important for making sure that interest rate rules can get the job done in monetary policy. In “Negative Interest Rate Policy as Conventional Monetary Policy,” in the posts I flag in “How and Why to Eliminate the Zero Lower Bound: A Reader’s Guide” and with Ruchir Agarwal, in “Breaking Through the Zero Lower Bound,” I arguethat eliminating any lower bound on interest rates is quite feasible, both technically and politically. Although this has not happened yet, the attitude of central bankers and economists toward negative interest rates and towards the paper currency policies needed to eliminate any lower bound on interest rates have shifted remarkably in the last five years. “Negative Interest Rate Policy as Conventional Monetary Policy” gave this list of milestones for negative interest rate policy up to November 2015:

1.     …. mild negative interest rates in the euro zone, Switzerland, Denmark and Sweden (see, for example, Randow, 2015).

2.     The boldly titled 18 May, 2015 London conference on ‘Removing the Zero Lower Bound on Interest Rates’, cosponsored by Imperial College Business School, the Brevan Howard Centre for Financial Analysis, the Centre for Economic Policy Research and the Swiss National Bank.

3.     The 19 May, 2015 Chief Economist’s Workshop at the Bank of England, which included keynote speeches by Ken Rogoff, presenting ‘Costs and Benefits to Phasing Out Paper Currency’ (Rogoff, 2014) and my presentation ‘18 Misconceptions about Eliminating the Zero Lower Bound’ (Kimball, 2015). …

4.     Bank of England Chief Economist Andrew Haldane’s 18 September, 2015 speech, ‘How low can you go?’ (Haldane, 2015).

5.     Ben Bernanke’s discussion of negative interest rate policy on his book tour (for Bernanke, 2015), ably reported by journalist Greg Robb in his Market Watch article ‘Fed officials seem ready to deploy negative rates in next crisis’ (Robb, 2015).

There have been at least four important milestones since then:

6.     Narayana Kocherlakota’s advocacy of a robust negative interest rate policy. (See Kocherlakota, February 1, February 9, June 9 and September 1, 2016.)

7.     The Brookings Institution’s June 6, 2016 conference “Negative interest rates: Lessons learned…so far” (video available at https://www.brookings.edu/events/negative-interest-rates-lessons-learned-so-far/ )

8.     The publication of Ken Rogoff’s book, The Curse of Cash.

9.     Marvin Goodfriend’s 2016 Jackson Hole talk “The Case for Unencumbering Interest Rate Policy at the Zero Bound” and other discussion of negative interest rate policy at that conference.

10.  Ben Bernanke’s embrace of negative interest rates as a better alternative than raising the inflation target in his blog post “Modifying the Fed’s policy framework: Does a higher inflation target beat negative interest rates?”

In addition, I can testify to important shifts in attitudes based on the feedback from central bankers in presenting these ideas at central banks around the world since May 2013 and as recently as December 2016.[1] One objective indicator of this has been increased access by proponents of a robust negative interest rate policy to high-ranking central bank officials.

2.     The Value of Large Movements in Interest Rates

Intuitively, the speed with which output gaps are closed and inflation fluctuations are stabilized depends is likely to depend on how dramatically a central bank is willing to move interest rates. It is notable that in explaining their monetary policy objectives, most central banks emphasize stabilizing inflation and unemployment, or stabilizing inflation alone.[2] But implicitly, many central banks act as if interest rate stabilization was also part of their mandates. This may be a mistake. The paper in this volume “The Yellen Rules” by Alex Nikolsko-Rzhevskyy, David H. Papell and Ruxandra Prodan provides suggestive evidence that increasing the size of the coefficients in the Taylor rule yields good outcomes; increasing the size of all the coefficients in the Taylor rule corresponds to increasing the size of interest rate movements. This is an idea that deserves much additional research.

For concreteness, let me talk about this as tripling the coefficients in the Taylor rule. Note that tripling the size of the coefficients in the Taylor rule only works on the downside if the lower bound on interest rates has been eliminated by changes in paper currency policy. Once the lower bound on interest rates has been eliminated, tripling the coefficients in the Taylor rule is likely to be a relatively safe experiment for a central bank to try. 

3.     Data Dependence in Both Directions

“Data dependence” has deservedly gained prominence as a central banking phrase. But in its current usage, “data dependence” of the action of a central bank at a given meeting almost always refers to incoming data determining either (a) whether the target interest rate will stay the same or go up in one part of the cycle, or (b) whether the target interest rate will stay the same or go down in another part of the cycle. Seldom does it refer to incoming data determining (c) whether the target interest rate stays the same, goes up or goes down. This is not the way formal models of optimal monetary policy work. If the target rate is where it should be at one meeting, there will be some optimal expected drift of the rate between that meeting and the next, but if meetings are relatively close together it would be strange if incoming news weren’t sometimes large enough to outweigh any such expected drift in the optimal policy. Indeed, if relevant news drove a diffusion process, the standard deviation of news would be proportional to the square root of the time gap between meetings, while the drift would be directly proportional to the time gap between meetings. Thus, when meetings are as close together as they are for most central banks (often as little as six weeks or one month), it would take quite large drift terms in the optimal policy to overcome the implications of news with such regularity that graphs of the target rate would take on the familiar stair-step pattern (going up the stairs, plateauing, then going down the stairs, and so on).

Indeed, I remember well a discussion with an economist at a foreign central bank in charge of calculating the implications of a formal optimal monetary policy rule. The rule had exactly the two-way character I am talking about, requiring the economist to add a fudge factor in order to get a one-way recommendation acceptable to the higher-ups.

One of the most important benefits of data dependence in both directions is that it allows more decisive movements in rates since it is considered easy to reverse course if later data suggests that move was too large. Indeed, the benchmark of optimal instrument theory with a quadratic loss function indicates that additive uncertainty does not affect the optimal level of the instrument. Thus, there is no need for a central bank that embraces “data dependence in both directions” to water down its reaction to a shock simply because it does not know what the future will bring. Staying put is more likely to be a big mistake than ignoring the uncertainty and going with the central bank’s best guess of the situation.

It is only when the effect size of the instrument itself is uncertain that movements in the instrument should be damped down. But one of the big advantages of interest rate policy—even negative interest rate policy—as compared to quantitative easing is that the size of the effect of a given movement in interest rates is much easier to judge given theory and experience than the effect of a given amount of long-term or risky asset purchases. Simple formal models predict that selling Treasury bills to buy long-term assets will have no effect, so any effect of quantitative easing is due to a nonstandard effect. Thus, any effect of such actions is due to one or more of many, many candidate nonstandard mechanisms. Theory then gives less guidance about the effects of quantitative easing than one might wish. And since the quantity of large scale asset purchases since 2008 was not enough to get economies quickly back on track, the relevant size of large scale asset purchases if one were to rely primarily on them in the next big recession is larger than anything for which we have experience. By contrast, in simple formal models, it is the real interest rate that matters for monetary policy. Monetary history provides a surprisingly large amount of experience with deep negative real rates. Other than paper currency problems that can be neutralized, only nonstandard mechanisms—such as institutional rigidities—would make low real rates coming from low nominal rates significantly different from low real rates coming from higher inflation.

One objection often made to “data dependence in both directions” is that reversing directions will make the central bank look bad—as if it doesn’t know what it is doing. A good way to deal with this communications problem is to spell out a formula in advance for how incoming data will determine the starting point for the monetary policy committee’s discussion of interest rates. Then it will be clear that it is the data itself that is reversing directions, not some central banker whim.

4. Stepping Away from Interest Rate Smoothing. The stair-step pattern of the target rate over time reflects not only an aversion to changing directions, but also an aversion to changing the interest rate too many basis points at any one meeting, where in the US the definition of “too many” is that traditionally, there is a substantial presumption against a movement of more than 25 basis points. The theoretical analogue of this behavior is often called “interest rate smoothing.” 

There is a myth among many macroeconomists that commitment issues make it sensible to tie the current level of the target rate to the past level of the target rate with interest rate smoothing. Commitment issues can make the drift term in the optimal monetary policy rule stronger and thereby tilt things somewhat toward a predominant direction of movement, but it is hard to see how they would penalize large movements in the target rate at a given meeting of the monetary policy committee. 

For “data dependence in both directions” and “stepping away from interest rate smoothing,” one need not embrace perfectly optimal monetary policy to get substantial improvements in monetary policy. Simply reducing the implicit penalty on changing directions or making a large movement in the target rate at a given meeting would bring benefits. 

5.     A More Equal Balance Between Output Stabilization and Inflation Stabilization

The Classical Dichotomy between real and nominal is akin to Descartes’ dichotomy between matter and mind. To break the mind-matter dichotomy, Descartes imagined that mind affected the body through the pineal gland (because it is one of the few parts of brain that does not come in a left-right pair). Where is the location analogous to the pineal gland where the Classical Dichotomy is broken in sticky price models? The actual markup of price over marginal cost (P/MC). For many sticky-price models, all the real part of the model needs to know is communicated by the actual markup (P/MC) acting as a sufficient statistic.[3] That is, if one takes as given the path of P/MC, one can often determine the behavior of all the relative prices and real quantities without knowing anything else about the monetary side of the model.

In cases where only one aggregate value for P/MC matters, the monetary model will differ from the real model it is built on top only in one dimension corresponding to the consequences of different values of P/MC. Thus, when duplicating the behavior of the underlying real model is attractive from the standpoint of welfare, all that is needed for excellent monetary policy is to choose the level of stimulus or reining in that yields the value of P/MC the underlying real model would have. Even when firm-level heterogeneity also matters for welfare, duplicating the aggregate behavior of the underlying real model is often an excellent monetary policy.

This logic is a big part of what lies behind the “divine coincidence” (Olivier Blanchard and Jordi Gali, 2007). That is, having, for many sticky-price models, only one dimension in which the vector of aggregate variables of the model can depart the vector of aggregate variables that would prevail in the underlying real model is a big part of the reason that the monetary policy that makes the output gap zero in those models also stabilizes inflation.

There are two main reasons the divine coincidence might fail. First, staying at the natural level of output generated by the underlying real model may not be the best feasible policy if there are fluctuations in the gap between the natural level of output and the ideal level of output (that would equate the social marginal benefit and social marginal cost of additional output).

Second, there may be more than one sectoral actual markup ratio P/MC that matters. Labor can be considered an intermediate good produced by its own sector far upstream, so sticky wages count as an additional sectoral price. But having sticky prices in the durables sector that follow a different path from sticky prices in the nondurables sector will also give the model more than one dimension in which it can depart from the underlying real model. The key to this second type of failure of the divine coincidence is fluctuations in the ratio between two different sticky-price aggregates.

When two aggregate markup ratios matter, it can be difficult for monetary policy to duplicate the behavior of the underlying real model. For monetary policy to keep the actual markups in two sectors simultaneously at the levels that would duplicate the behavior of the underlying real model even in the face of frequent shocks, monetary policy would have to be based on two instruments different enough in their effects that they could have a two-dimensional effect on the economy.

When the divine coincidence fails, there is a tradeoff between stabilizing output and stabilizing inflation. Then it becomes important to know how bad output gaps are compared to aggregate price fluctuations. Much of the cost of output gaps is quite intuitive: less smoothing of labor hours. The cost of departures from steady inflation are a little less intuitive: in formal models the main cost of price fluctuations is intensified leapfrogging of various firms’ prices over each other that can lead people to go to stores or to products that make no sense from an efficiency point of view. This cost of leapfrogging prices causing inefficient purchasing patterns is proportional to how responsive people are to prices. The higher the price elasticity of demand, the bigger the misallocations from the microeconomic price disturbances caused by leapfrogging prices when macroeconomic forces make aggregate prices to fluctuate.

It is common in optimal monetary policy models to calibrate the price elasticity of demand at the firm level to a quite high value—often as high as 11. Where does this relatively high number come from? I have a suspicion. Susanto Basu and John Fernald (1996, 2002) and Basu (1997) estimate average returns to scale in the US economy of 1.1. Given free entry and exit of monopolistically competitive firms, in steady state average cost (AC) should equal price (P): if P > AC, there should be entry, while if P < AC there should be exit, leading to P=AC in steady state. Price adjustment makes marginal cost equal to marginal revenue in steady state. Thus, with free entry, in steady state,

where by a useful identity[4] γ is equal to the degree of returns to scale and μ is a bit of notation for the desired markup ratio P/MR. The desired markup ratio is equal in turn to the price elasticity of demand epsilon divided by epsilon minus one: 

Thus, a returns-to-scale estimate of γ=1.1 implies a price elasticity of demand ε11.

There are several holes in this logic. First, the average returns-to-scale estimate of 1.1 is suspect. Disaggregating by sectors in Basu, Fernald and Kimball (2006), the returns to scale estimate for nondurable manufactures was .87, and within durables production, lumber was .51. This is implausible. Tjalling Koopmans argued persuasively that if all factors are accounted for, and plenty of each factor is available, a production process can always be replicated, guaranteeing that constant returns to scale are possible. That is, if all factor prices are held constant, twice as much output can always be produced at twice the cost by doubling all inputs and doing the same thing all over again. It may be possible to do better—increasing returns to scale—but the firm will never have to do worse than replicating its production process. Therefore, returns to scale are at least constant when defined by what happens to costs with increases in scale when factor prices are held fixed.

Why might the estimate of returns to scale for nondurables come in at .87, and for lumber .51? There is more than one possible answer, but an obvious possibility is that in the boom, firms need to employ worse quality inputs, while in the bust, firms only hang onto the best quality inputs. It is not possibly to fully adjust for input quality using the available indicators of quality. So what looks like 1% increase in inputs might be only a .87% increase in quality-adjusted inputs or less if one could only adjust for unmeasured quality. If the quality profile of hiring and layoffs remains similar in many different circumstances, the false returns-to-scale estimate of .87 for nondurables might still be useful for isolating movements in productivity from these regular patterns of expansion and contraction of scale with accompanying changes in quality, but the false returns-to-scale estimate is not appropriate as part of the average for estimating the  that should be equal to the desired markup ratio  in the long run if there is free entry and exit.

Moreover, given the logic of using only the very best inputs in the bust, but worse inputs in the boom, the bias that affects nondurables manufacturing is likely to affect other sectors as well. Thus, true returns to scale and therefore the markup ratio could be much bigger than 1.1. The bigger the markup ratio, the lower the implied price elasticity of demand and the lower the costs from leapfrogging prices causing inefficient purchases.

Another reason the desired markup ratio may be underestimated—and therefore the price elasticity of demand therefore overestimated—is that firms face substantial sunk costs in entering a market. For example, John Laitner and Dmitriy Stolyarov (2011) emphasize the high failure rate in the first few years of a new business. This high failure rate is likely to deter entry in a way that will not show up in any observed flow fixed cost once the business is a solidly going concern. Therefore, one can expect that price will be above the observed average cost. Yet the observed average cost is what is relevant for estimates of returns to scale from looking at what happens to going concerns in booms and busts. Thus, P > AC implies that mu>gamma even for the true gamma when the true gamma is interpreted in this way as what happens when going concerns vary their scale.

Finally, the price elasticity of demand that bears a long-run relationship to the degree of returns to scale is the long-run price elasticity of demand. But the price elasticity of demand that matters for leapfrogging prices causing inefficient purchases is the short-run price elasticity of demand. The short-run price elasticity of demand is likely to be much smaller than the long-run price elasticity of demand. This gives one more reason why optimal monetary policy models with common calibrations might overestimate the welfare cost of inefficient purchases caused by the leapfrogging prices accompanying aggregate price fluctuations. Thus, it is possible that the cost of output gaps is of roughly the same size as the cost of price fluctuations rather than being significantly smaller as common calibrations imply.

6.     The Importance of Durables

In “Sticky Price Models and Durable Goods,” Robert Barky, Chris House and I show that as soon as a sticky price model has a durable goods sector (which many do not) it is sticky prices for durable goods that give monetary policy its power. Sticky prices in nondurables only reduce the power of monetary policy greatly, and lead to negative comovement durables and aggregate output. This importance of durables prices for sticky-price models suggests that durables prices ought to also be important for monetary policy. Indeed, Barsky, Christoph Boehm, House and Kimball (2016) argue that the price index a central bank tries to stabilize should have a weight on durables larger than the weight of durables in GDP. By contrast, some central banks pay most attention to the consumption deflator, which has a much smaller weight on durable goods prices than the weight of durables in GDP.

The importance of this for monetary policy can be illustrated by the impulse responses in Basu, Fernald, Jonas Fisher and Kimball (2013). There, technology improvements in the nondurables and services sector are estimated to expand employment, while technology improvement in the durable goods sector lead to lower employment. Why might this be? A simple story is that the Fed is staring at the consumption deflator. When there is an improvement in nondurables and services technology, this shows up in a lower consumption deflator, and the Fed provides some stimulus to restore the consumption deflator to it target growth rate. When there is an improvement in durables technology, particularly for business equipment, the consumption deflator is affected much less. Therefore, the Fed does not accommodate as much, and the ability to produce more output with the same inputs instead leads to something closer to producing the same output with fewer inputs. If this is true, it points to a serious problem with focusing primarily on a price index that has a low weight on durables.

There is another message for research on monetary policy. Including a durable goods sector in monetary policy models is crucial. Too much of the literature does not do this. Adding durables goods sectors to monetary policy models should be a big part of the research agenda in the coming decade. Moreover, models with a durable goods sector should explore a variety of parameter values: parameter values that make the durable goods sector more important for the results as well as parameter values that keep the durable goods sector relatively tame so that it does not affect results much.

7.     Adjusting for the Risk Premium

Vasco Curdia and Michael Woodford (2010) argue that the usual target rate—assumed to be a safe short-term interest rate—should drop by about 80% of the rise in the risk premium—say as measured by the spread between the T-bill repo rate and the commercial paper rate. If borrowers have a much higher elasticity of intertemporal substitution than savers, the recommended percentage of compensation for a rise in the risk premium could get even higher, getting close to what is effectively a commercial paper rate target. It would be very helpful for central banks to bring this kind of thinking explicitly into policy-making.

There are two other points to make here. First, note that having something close to an effective commercial paper rate target would do much of what people saying interest rate policy should respond to financial stability concerns want in practice, but for a different reason that does not depend on any fear of disaster. Second, when the risk premium rises dramatically, following such a policy requires having eliminated the lower bound on interest rates—one more way in which eliminating the lower bound on interest rates is foundational for next generation monetary policy.

8.     Coordination with Financial Stability

Beyond the compensation for movements in the risk premium discussed above, let me argue that if financial stability concerns are significantly affecting interest rate policy, other tools to enhance financial stability are being underused. Here, my perspective is strongly influenced by Anat Admati and Martin Hellwig’s The Banker’s New Clothes. They make the case that there is very little social cost to strict leverage limits on financial firms. John Cochrane (2013), in his review of The Banker’s New Clothes, writes memorably:

Capital is not an inherently more expensive source of funds than debt. Banks have to promise stockholders high returns only because bank stock is risky. If banks issued much more stock, the authors patiently explain, banks' stock would be much less risky and their cost of capital lower. "Stocks" with bond-like risk need pay only bond-like returns. Investors who desire higher risk and returns can do their own leveraging—without government guarantees, thank you very much—to buy such stocks. …

Why do banks and protective regulators howl so loudly at these simple suggestions? As Ms. Admati and Mr. Hellwig detail in their chapter "Sweet Subsidies," it's because bank debt is highly subsidized, and leverage increases the value of the subsidies to management and shareholders. To borrow without the government guarantees and expected bailouts, a bank with 3% capital would have to offer very high interest rates—rates that would make equity look cheap. Equity is expensive to banks only because it dilutes the subsidies they get from the government. That's exactly why increasing bank equity would be cheap for taxpayers and the economy, to say nothing of removing the costs of occasional crises. …

How much capital should banks issue? Enough so that it doesn't matter! Enough so that we never, ever hear again the cry that "banks need to be recapitalized" (at taxpayer expense)!

I have yet to hear a persuasive argument that the social as opposed to the private cost of strict leverage limits are anything to be concerned about. There are only two concerns that come close. First, it may be important to cut capital taxation in other ways to compensate for the higher effective tax rates when firms have more equity. But this is a plausible political tradeoff to make as part of a legislative package that dramatically raises capital requirements. Second, the reduced subsidy to financial firms could reduce aggregate demand. But eliminating the zero lower bound guarantees that there will longer be any shortage of aggregate demand.

But what if the interest rate cuts that bring aggregate demand back up themselves hurt financial stability? The answer is that if leverage limits are strict enough, this is unlikely to be a problem. One hears arguments (a) that interest rates can’t be cut because it will hurt financial stability, and (b) that capital (equity-finance) requirements can’t be raised because they will hurt aggregate demand. However, as long as, in absolute values, the ratio of aggregate demand to financial stability effects of interest rate cuts is larger than the ratio of aggregate demand to financial stability effects of higher capital requirements. This can be seen from the following diagram, taken from my blog post “Why Financial Stability Concerns Are Not a Reason to Shy Away from a Robust Negative Interest Rate Policy.”

The diagram above shows that, as long as interest rate cuts—which are primarily intended to effect aggregate demand—and higher equity requirements—which are primarily intended to affect financial stability—each have intended effects that are bigger than their side effects, then a combination of interest rate cuts with increases in equity requirements will both increase aggregate demand and improve financial stability. Careful study of the diagram indicates that what is crucial is that the vector of effects from interest rate cuts have a smaller negative slope than the vector of effects from higher equity requirements; if that condition is satisfied, getting the relative dosages of lower rates and higher equity requirements will both increase aggregate demand and improve financial stability.

Though they do not act alone, the Fed and other central banks have significant influence over the level of capital requirements. They should use their influence in this area vigorously to push for higher capital requirements, both for the direct benefits of higher financial stability and to free up interest rate policy to close output gaps and stabilize inflation.

9.     A Nominal Anchor

My understanding of the importance of nominal anchors is more second-hand and impressionistic than I would like. But it seems that many who study monetary policy have argued for targeting a path for prices as opposed to a level for inflation. Others have argued for targeting the velocity-adjusted money supply, also known as nominal GDP. Both ideas involve having a nominal anchor for monetary policy. During the Great Recession, either type of nominal anchor would have led to a rule that recommended more monetary stimulus than major economies in fact received—a recommendation that looks good in hindsight.

It is also my impression that nominal anchors make monetary policy rules “stable” in the theoretical sense to a wider set of shocks and under a wider range of solution concepts than monetary policy rules that do not have nominal anchors. Our ignorance about the future shocks economies and which solution concepts are appropriate make that kind of robust theoretical stability valuable.

If price-level targets are explained in terms of their implications for inflation, they seem unintuitive and even dangerous to many people, since viewed through that lens they call for “catch-up” inflation if inflation has been below the growth rate of the price-level target. Someday, after the lower bound on interest rates has been eliminated, it may be possible to deal with this communications problem by having a target of absolute price stability, in which the price level target does not change at all (within the limits of how well aggregate prices can be measured). An unchanging price-level target is much easier to explain to the public than a moving price-level target.

Advocates of a nominal GDP target have demonstrated that a nominal GDP target can be explained reasonably well. I do not think a nominal GDP target faces any insuperable communications difficulties.

An Example of an Interest Rate Rule Along the Lines of These Principles

Primarily as a way of illustrating the ideas above, let me set down the following interest-rate rule:

where

and g is a periodically revised estimate of the current trend growth rate of potential (natural) real GDP, determined as the median of all the values put forward by each member of the monetary policy committee.

Note that the coefficient of 1.5 on log nominal GDP is equivalent to a coefficient of 1.5 on log real GDP and a coefficient of 1.5 on the log GDP deflator. Thus, it includes both a tripling of the regular Taylor rule coefficient on log real GDP and a coefficient of 1.5 on the log price level in order to provide a nominal anchor. One way in which the nominal anchor here provides additional stability is that if the estimate of the natural level of output is off, the movement of the price level will still eventually restore a reasonable interest rate rule. If g is wrong as an estimate of the growth rate of natural output, it should be possible to eventually discover and correct that. If not, a persistent error in g could lead to inflation persistently away from the target of zero. But things still would not spiral out of control: the inflation rate would simply be away from target by the amount of the persistent error in g.

The Potential of Interest Rate Policy

The picture I want to paint is of the possibility of a monetary policy rule that would be much better than the monetary policy rules we have become used to. Much is uncertain. Research that hasn’t been done yet must be followed by trial runs yet to be conducted on the most promising ideas. But it seems possible interest rate policy could close output gaps and stabilize inflation within about a year—that is, with the speed of getting the economy back on track limited only by the well-known 9- to 18-month lag in the effect of monetary policy. And for shocks that have some forewarning, that 9- to 18-month clock can start from the moment of that forewarning.

With no effective lower bound on interest rates, there will be no need to conduct open market operations in anything but T-bills. There will be no need for fiscal stabilization beyond automatic stabilizers and possibly “national lines of credit” to households a la Kimball (2012) to stimulate the economy in the period before monetary policy stimulus kicks in given its lag.

One level of success would be to return to the Great Moderation. A higher level of success would be stay at the natural level of output all the time, except for the period between the arrival of a shock and when the effects of monetary policy kick in. A bit higher level of success would be to essentially solve the monetary policy problem.

Of course, solving the monetary policy problem does not mean all our problems are solved! The long-run Classical Dichotomy means that long-run economic growth depends on other policies. And although it might help, economic growth alone cannot solve the problems of war and peace, nor answer the question of what our highest human objectives should be.

However, for those of us who have spent or are spending an important part of our individual careers in trying to improve monetary policy, helping to understand and implement the principles of next generation monetary policy is a worthy endeavor indeed.

[1] See https://blog.supplysideliberal.com/post/53171609818/electronic-money-the-powerpoint-file for a list of these seminars.

[2] The Fed’s mandate is “to promote effectively the goals of maximum employment, stable prices, and moderate long-term interest rates.” Moderate long-term interest rates come from low inflation. And term-structure relationships make stable long-term interest rates consistent with sharp movements in short-term interest rates for short periods of time.

[3] The actual markup P/MC should be distinguished from the desired markup: price over marginal revenue P/MR. The desired markup mainly matters for price-setting, and is one of the ingredients that determines the actual markup P/MC.

References

Agarwal, Ruchir, and Miles Kimball, 2015. “Breaking Through the Zero Lower Bound,” IMF Working Paper 15/224.

Admati, Anat, and Martin Hellwig, 2013. The Banker’s New Clothes: What’s Wrong with Banking and What to Do about It, Princeton University Press.

Barsky, Robert, Christoph Boehm, Chris House and Miles Kimball, 2016. “Monetary Policy and Durable Goods,” Federal Reserve Bank of Chicago Working Paper No. WP-2016-18.

Barsky, Robert, Chris House, and Miles Kimball, 2007: “Sticky-Price Models and Durable Goods,” American Economic Review, 97 (June), 984-998.

Basu, Susanto, 1997. “Returns to Scale in U.S. Production: Estimates and Implications.” Journal of Political Economy 105 (April), pp. 249-83.

Basu, Susanto, and John Fernald, 1996. “Procyclical Productivity: Increasing Returns or Cyclical Utilization?” Quarterly Journal of Economics 111 (August), pp. 719-51.

Basu, Susanto, and John Fernald, 2002. “Aggregate Productivity and Aggregate Technology.” European Economic Review 46 (June), pp. 963-991.

Basu, Susanto, John Fernald and Miles Kimball, 2006. “Are Technology Improvements Contractionary?” American Economic Review 96 (December), pp. 1418-1448.

Basu, Susanto, John Fernald, Jonas Fisher, and Miles Kimball, 2013. “Sector-Specific Technical Change.” Federal Reserve Bank of San Francisco mimeo.

Bernanke, Ben, September 2016. “Modifying the Fed’s policy framework: Does a higher inflation target beat negative interest rates?” Ben Bernanke’s blog https://www.brookings.edu/blog/ben-bernanke/2016/09/13/modifying-the-feds-policy-framework-does-a-higher-inflation-target-beat-negative-interest-rates/#cancel

Blanchard, Olivier and Jordi Gali, 2007. “Real Wage Rigidities and the New Keynesian Model”
Journal of Money, Credit, and Banking, supplement to vol. 39 (1), 2007, 35-66

Cochrane, John, March 1, 2013. “Running on Empty: Banks should raise more capital, carry less debt—and never need a bailout again,” Wall Street Journal op-ed.

Curdia, Vasco, and Michael Woodford, 2010. "Credit Spreads and Monetary Policy," Journal of Money, Credit and Banking, Blackwell Publishing, vol. 42 (1), 3-35

Kimball, Miles, (2012). “Getting the Biggest Bang for the Buck in Fiscal Policy,” pdf available at https://blog.supplysideliberal.com/post/24014550541/getting-the-biggest-bang-for-the-buck-in-fiscal recommended over the NBER Working Paper 18142 version.

Kimball, Miles, originally 2013, regularly updated. “How and Why to Eliminate the Zero Lower Bound,” https://blog.supplysideliberal.com/post/62693219358/how-and-why-to-eliminate-the-zero-lower-bound-a

Kimball, Miles, 2015. “Negative Interest Rate Policy as Conventional Monetary Policy,” National Institute Economic Review, 234:1, R5-R14.

Kimball, Miles, 2016. “Why Financial Stability Concerns Are Not a Reason to Shy Away from a Robust Negative Interest Rate Policy,” Confessions of a Supply-Side Liberal blog, https://blog.supplysideliberal.com/post/144132627184/why-financial-stability-concerns-are-not-a-reason

Kocherlakota, Narayana, February 1, 2016. “The Potential Power of Negative Nominal Interest Rates” https://sites.google.com/site/kocherlakota009/home/policy/thoughts-on-policy/2-1-16

Kocherlakota, Narayana, February 9, 2016. “Negative Rates: A Gigantic Fiscal Policy Failure” https://sites.google.com/site/kocherlakota009/home/policy/thoughts-on-policy/2-9-16

Kocherlakota, Narayana, June 9, 2016. “Negative Interest Rates Are Nothing to Fear,” Bloomberg View https://www.bloomberg.com/view/articles/2016-06-09/negative-interest-rates-are-nothing-to-fear

Kocherlakota, Narayana, September 1, 2016. “Want a Free Market? Abolish Cash,” Bloomberg View https://www.bloomberg.com/view/articles/2016-09-01/want-a-free-market-abolish-cash

Laitner, John and Dmitriy Stolyarov, 2011. “Entry Conditions and the Market Value of Businesses,” University of Michigan mimeo.

Reis, Ricardo (2017) “Funding Quantitative Easing to Target Inflation” in Designing Resilient Monetary Policy Frameworks for the Future, Federal Reserve Bank of Kansas City.

Rogoff, Kenneth, August 2016. The Curse of Cash, Princeton University Press.