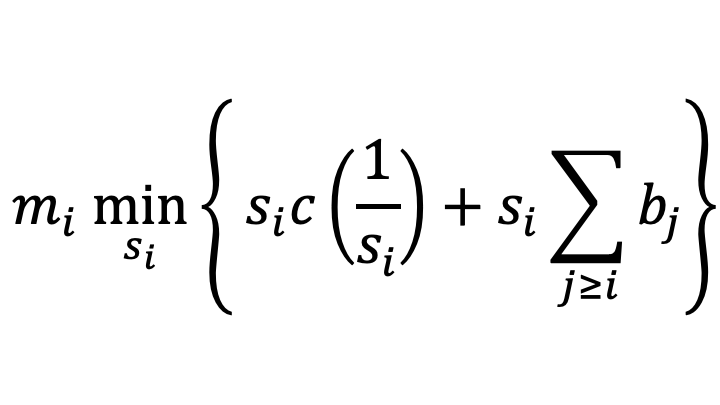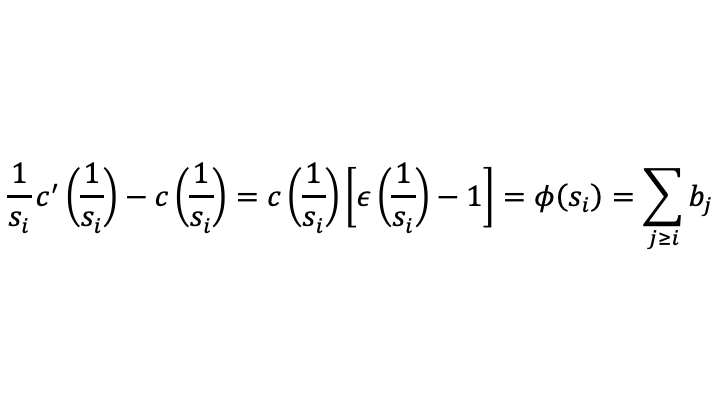In “How Fast Should a Project Be Completed?” I asked the question of how fast to do a project it does nothing for you when half-finished, but yields a continuing stream of benefits from the moment it is completed. My conclusion was the a project of that type should be completed quite fast unless the elasticity of the cost with respect to rate of progress gets high.

My example of a project was my efforts to learn German, with the idea that it will only be attractive to read German for fun once I have learned a vocabulary of 10,000 German words (using the methods I discuss in “The Most Effective Memory Methods are Difficult—and That's Why They Work”).

But I actually want to learn French and Spanish as well as German. What is the best way to approach multiple projects. For this post, I’ll assume each has a flow of benefits once completed, and not before, and that these benefits are additively separable, with no crowding out.

Let me first set out the notation:

Where it says “annual cost” above, it could have just as well said “daily cost,” because I assume that costs are additively separable across time and the model is in continuous time. That also means there is no direct production efficiency to be gained from working on more than one project at a time. Also, in this problem, all the efforts are under one’s own control—no waiting for coauthors or for a journal to get back to you. Needing to wait for someone else could be a reason to mix it up by working on another project while waiting for input on one.

The objective is to minimize total cost:

Total Cost = Cost of Completing Projects + Cost of Delay in Getting the Benefits from Completed Projects

Using the notation laid out above,

It is not a difficult task to show that given these assumptions circumstance, it is best to work on just one project at a time. For example, it can’t be optimal to be working on the first completed task and the second completed task at the same time. Just keep the pace of doing each project the same and do some rearrangement of effort timing to get the first project done sooner, without changing the moment at which both of the first two projects are completed. This will be better. The possibility of another rearrangement shows that you shouldn’t work on the third or any later completed task before the first task is completed. So only work on the first until it is done. Then consider all the projects after the first one and use the same argument over again.

So projects should be pursued one at a time here. What order should they be done in. Notationally, I have written things with numbers representing the sequencing of projects that is, in fact, optimal. But there are some necessary conditions for a proposed sequencing of projects to be optimal. In particular, it can’t be an optimal sequencing if it is possible to switch the order of two consecutive projects—holding the slowness with which each project is pursued—and reduce the total cost. Let’s call those two consecutive projects A and B. If the time it takes to do each project is held constant, then the path of the flow of benefits from projects completed before A and B won’t change and the path of the flow of benefits from projects completed after A and B won’t change, since the time when each of the other projects is completed and begins throwing off benefits is unchanged. Even for A and B, the time needed to complete all the previous projects is unchanged, and so can be ignored when considering whether switching the order of those two.

Thus, the order A, then B, can only be optimal if:

Subtract this from both sides of the inequality:

That yields this expression of the inequality necessary for A, then B to be optimal:

Changing the sign and taking the reciprocal preserves the direction of the inequality:

Finally, multiply by the product of the benefit flows of A and B and switch right and left to obtain this necessary condition for the order A, then B to be optimal:

This is a necessary condition because otherwise, switching the order of A and B while hold the slowness for A and the slowness for B fixed would reduce total cost. If the slownesses were all exogenously given, this condition for each consecutive pair would also be sufficient, since then—other than ties with equality on this condition—there is only one way to get an order that satisfies the necessary condition. If the slownesses were exogenously given, the projects should be done from the exogenous highest benefit/time required ratio b/[ms] to the lowest.

If the slownesses are endogenous, things are more complex. It is possible for both [A, then B] and [B, then A] to satisfy the necessary condition because, as I’ll show in a second, putting something earlier in the order increases the optimal speed—and reduces the optimal slowness—with which a project should be done. The reason is intuitive: the earlier a project is in the order, the more other projects are waiting for that early project to be completed, making it more urgent. Look closely and you can see that if the slowness of B is lower in the [B, then A] order, then the necessary condition might be satisfied for both [A, then B] and [B, then A]. And the sufficient condition is beyond the scope of this particular post. Nevertheless, the necessary condition above means that at the optimal slownesses and optimal sequencing, the benefit to required time ratio monotonically declines from one project to the next.

Now let me back up my claim that projects earlier in the sequence should be done faster. Pulling out the terms in the expression for total cost that involve s_i isolates the optimization subproblem for s_i. The optimal slowness is thus the solution to this optimization subproblem:

The magnitude of the project drops out of the first-order condition:

Calculating the first derivative of the function phi shows that it is is downward sloping in slowness s_i:

That justifies the way I have the graph at the top of this post. The greater the sum of benefits from this project and all subsequent projects, the faster this project should be done. (Faster = less slowly, lower s_i.)

Note that if the benefits of completion are not additive so that the marginal product of each project depends on the order, it makes it more complex to determine the right order, given any order the implication that earlier projects will optimally go at a quicker pace remains. Whatever the marginal product of later projects (assuming those marginal products are positive), those marginal products of later projects will add to the urgency of completing the first project in order to more expeditiously move on to later projects.

So I should study German even faster, given that I have French and Spanish lined up to study after that.