I was very interested to learn that colleague Adam McCloskey and his coauthor Pascal Michaillat had a paper that can be seen as backing up the idea that a t-statistic of 3 would be a useful critical value for us to impose as a rule in the social sciences—an idea I write about in “Let's Set Half a Percent as the Standard for Statistical Significance.” (However, setting a standard that appears to be a p-value of half a percent that way things are usually talked about is really something close to setting a 5% standard that is robust to p-hacking.) Below is a guest post from Adam, distilling the message of his paper with Pascal: “Incentive Compatible Critical Values.”

Motivated by the replicability crisis occurring across the sciences, Pascal Michaillat and I set out to produce a means of assessing statistical significance that is immune from the all-too-common phenomenon of p-hacking. 

Broadly speaking, p-hacking refers to a researcher searching through data, model specifications and/or estimation methods to produce results that can be considered statistically significant.  This behavior can take on many forms such as collecting additional data and examining multiple regression specifications. 

There is now a large body of research showing that p-hacking is quite pervasive in empirical research in economics and across many other scientific fields.  This fact presents a major problem for scientific credibility and replicability since our standard means of assessing whether data support a scientific hypothesis assume away this type of behavior.  Indeed, the standard distributions (e.g., standard normal) to which we compare test statistics (e.g., t statistics) to assess significance are justified upon the presumption that the test statistics were constructed from a single data set, model specification, and estimator. 

In other words, the tools empirical researchers use every day to assess whether a finding is merely a result of chance are ill-suited to the very behavior these researchers engage in.  This fact mechanically leads researchers to find spurious “discoveries” at a rate much higher than conventionally acceptable levels, such as 5%, and an inability for other researchers to replicate such “discoveries”.

Ours is certainly not the first attempt to overcome this problem of hypothesis test over-rejection resulting from p-hacking.  Several admirable proposals have been made and, in some cases implemented, ranging from constraining researcher behavior via pre-analysis plans to raising the bar for whether a finding ought to be deemed statistically significant.

However, there are limitations to each of these.  Pre-analysis plans are not entirely enforceable, are very difficult to implement with the observational data that researchers are commonly limited to and, perhaps most importantly, do not allow researchers to use their data to explore which questions may be interesting to address in the first place.  Using data to search for interesting problems is often done with the best intentions for scientific progress: data can help us to discover new and important hypotheses to test.  

Another recent proposal to mitigate p-hacking is to reduce conventional significance levels from 5% to 0.5%. However, it is reasonable to worry that mechanically raising the bar for statistical significance can lead to a statistical significance arms race in which researchers continue to p-hack until finding a result that crosses the more stringent statistical criterion.

In our paper, “Incentive-Compatible Critical Values,” we propose to let the incentives of researchers enter the calculation for whether a result ought to be deemed statistically significant.  Since the vast majority of empirical results that journals choose to publish are rejections of a null hypothesis, we assume that a researcher will continue to conduct “studies” until finding a statistically significant rejection, or until the benefit from conducting an additional study falls below the cost.  Here, “studies” can take many forms that range from collecting additional data to changing model specifications or estimation methods. 

In our framework, as in practice, a finding is determined statistically significant when the test statistic used to test the finding exceeds a critical value threshold.  In addition to the costs of conducting research and the benefits of publishing, we note that the number of studies a researcher will choose to conduct is a function of (among other things) this critical value: if the critical value is small, the researcher has the incentive to conduct multiple studies, while if it is too large, she may not conduct any studies at all.    

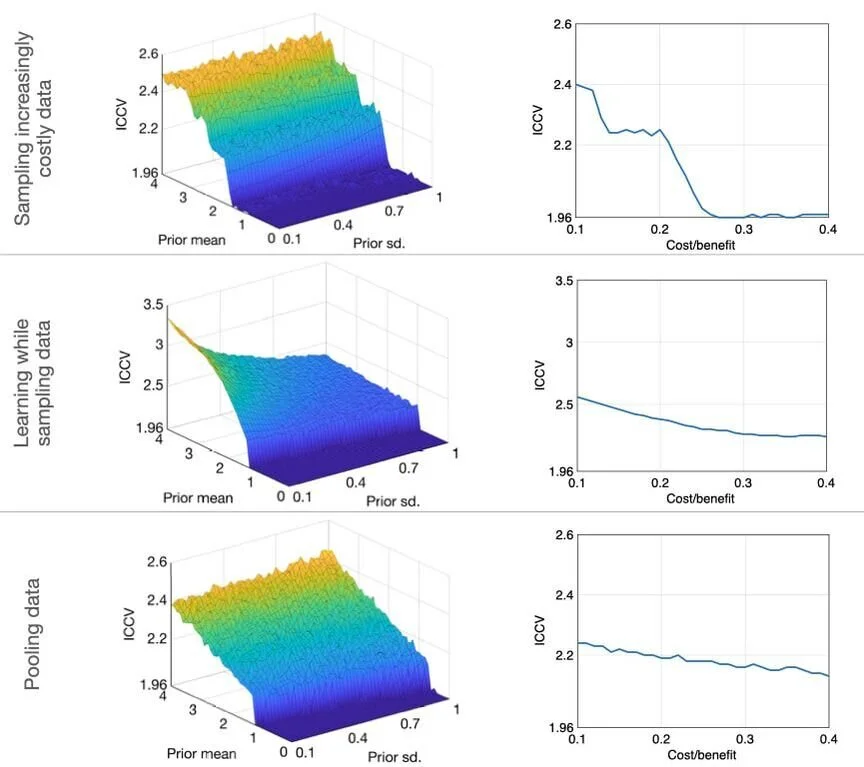
Rather than constructing this critical value under the classical assumptions we know are violated in practice, we account not only for the fact that researchers respond to critical value thresholds by conducting multiple studies to search for significance but also that it is costly to do so.  Given the endogenous response of researchers, we propose the use of a critical value at which the probability of finding a statistically significant result can be controlled at a conventionally acceptable level, such as 5%.  This amounts to solving a fixed-point problem to find the Incentive-Compatible Critical Value (ICCV).

We calibrate the costs and benefits of conducting studies as well as the researcher’s subjective beliefs to an experimental setting and calculate the ICCV under various scenarios for how the researcher combines the data she obtains in each successive experiment and updates her beliefs about the truth as she collects more data.  We then perform a sensitivity analysis to look across fairly wide ranges of costs, benefits and researcher beliefs centered on our empirical calibration. 

Since they allow researchers to search for significance across multiple studies, the ICCVs are necessarily larger than classical critical values (e.g., 1.96).  Yet, for the broad range of researcher behaviors and beliefs we examine, they lie in a fairly narrow range (see figure).  For a two-sided t-test with a level of 5%, we calculate the ICCV range to equal about 1.96 to 3.  In other words, a critical value equal to about 3 limits false rejection probabilities to 5% in experimental settings across a wide range of researcher behaviors and beliefs.

Looking forward, more data measuring the costs and benefits of research and researchers’ subjective beliefs across various scientific disciplines and methodologies would be extremely valuable for computing appropriate tailor-made ICCVs.